题目内容
 如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C,若∠A=35°,则∠ABX+∠ACX的度数是
如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C,若∠A=35°,则∠ABX+∠ACX的度数是
- A.25°
- B.35°
- C.45°
- D.55°
D
分析:根据三角形的内角和定理可得出在三角形ABC中,∠ABC+∠ACB=180°-35°,在三角形BCX中∠XBC+∠XCB=90°,从而得出答案.
解答: 解:∵∠X=90°,
解:∵∠X=90°,
∴∠XBC+∠XCB=90°,
∵∠A=35°,
∴∠ABC+∠ACB=180°-35°=145°,
∴∠ABX+∠ACX=(∠ABC+∠ACB)-(∠XBC+∠XCB)=145°-90°=55°.
故选D.
点评:本题考查了三角形的内角和定理,三角形的内角和等于180度,是基础知识比较简单.
分析:根据三角形的内角和定理可得出在三角形ABC中,∠ABC+∠ACB=180°-35°,在三角形BCX中∠XBC+∠XCB=90°,从而得出答案.
解答:
 解:∵∠X=90°,
解:∵∠X=90°,∴∠XBC+∠XCB=90°,
∵∠A=35°,
∴∠ABC+∠ACB=180°-35°=145°,
∴∠ABX+∠ACX=(∠ABC+∠ACB)-(∠XBC+∠XCB)=145°-90°=55°.
故选D.
点评:本题考查了三角形的内角和定理,三角形的内角和等于180度,是基础知识比较简单.

练习册系列答案
相关题目
 5、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C,若∠A=35°,则∠ABX+∠ACX的度数是( )
5、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C,若∠A=35°,则∠ABX+∠ACX的度数是( )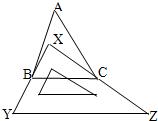 2、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABX+∠ACX=
2、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABX+∠ACX=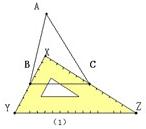 26、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=40°,则∠XBA+∠XCA=
26、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=40°,则∠XBA+∠XCA=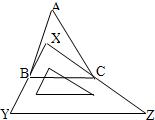 6、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C、△ABC中,∠A=30°,则∠ABX+∠ACX=( )
6、如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C、△ABC中,∠A=30°,则∠ABX+∠ACX=( )