ΧβΡΩΡΎ»ί
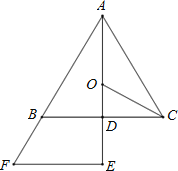
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΝβ–ΈABCD÷–Θ§![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Ζ÷±π «Νβ–ΈABCDΒΡΝΫΧθΕ‘Ϋ«œΏ≥ΛΚΆ±Ώ≥ΛΘ§’β ±Έ“Ο«Α―ΙΊ”Ύ
Ζ÷±π «Νβ–ΈABCDΒΡΝΫΧθΕ‘Ϋ«œΏ≥ΛΚΆ±Ώ≥ΛΘ§’β ±Έ“Ο«Α―ΙΊ”Ύ![]() ΒΡ–Έ»γΓΑ
ΒΡ–Έ»γΓΑ![]() Γ±ΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ≥ΤΈΣΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±Θ°«κΫβΨωœ¬Ν–Έ ΧβΘΚ
Γ±ΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χ≥ΤΈΣΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±Θ°«κΫβΨωœ¬Ν–Έ ΧβΘΚ

Θ®1Θ©ΧνΩ’ΘΚΔΌΒ±![]() Θ§
Θ§![]() ±Θ§
±Θ§![]() Θ°
Θ°
ΔΎ”ΟΚ§![]() Θ§
Θ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ
ΒΡ¥ζ ΐ Ϋ±μ Ψ![]() ÷ΒΘ§
÷ΒΘ§![]() Θ°
Θ°
Θ®2Θ©«σ÷ΛΘΚΙΊ”Ύ![]() ΒΡΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±
ΒΡΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±![]() ±Ί”– Β ΐΗυΘΜ
±Ί”– Β ΐΗυΘΜ
Θ®3Θ©»τ![]() «ΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±
«ΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±![]() ΒΡ“ΜΗωΗυΘ§«“Νβ–ΈΒΡΟφΜΐ «25Θ§BE «Νβ–ΈABCDΒΡAD±Ώ…œΒΡΗΏΘ§«σBEΒΡ÷ΒΘ°
ΒΡ“ΜΗωΗυΘ§«“Νβ–ΈΒΡΟφΜΐ «25Θ§BE «Νβ–ΈABCDΒΡAD±Ώ…œΒΡΗΏΘ§«σBEΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ5Θ§ΔΎ![]() ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©
ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫαΚœΆΦ–ΈΘ§ΗυΨίΝβ–ΈΒΡΕ‘Ϋ«œΏΜΞœύΤΫΖ÷“‘ΦΑΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©Υψ≥ωΓςΘ§ΫαΚœΘ®1Θ©÷–ΔΎΒΡΫα¬έΦ¥Ω…ΫβΨωΈ ΧβΘΜ
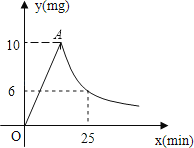
Θ®3Θ©ΗυΨίΖΫ≥ΧΗυΒΡΕ®“εΒΟ≥ωmΓΔnΓΔtΒΡΙΊœΒΘ§ΫαΚœΘ®1Θ©÷–ΔΎΒΡΫα¬έΫχ––Μ·ΦρΘ§‘ΌΗυΨίΝβ–ΈΟφΜΐ «25Θ§Φ¥Ω…ΒΟ≥ωtΒΡ÷ΒΘ§ΫχΕχΒΟ≥ωΫα¬έΘ°
Θ®1Θ©ΔΌΒ±m=6Θ§n=8 ±Θ§AO=4Θ§OB=3Θ§Γύt=AB=![]() =5Θ°
=5Θ°
ΔΎΓΏAO=![]() Θ§OB=
Θ§OB=![]() Θ§Γύt2=AB2=
Θ§Γύt2=AB2=![]() Θ°
Θ°
Ι ¥πΑΗΈΣΘΚ5Θ§![]() Θ°
Θ°
Θ®2Θ©![]()
’βάοΘ§a=mΘ§b=![]() tΘ§c=nΘ§Γύ
tΘ§c=nΘ§Γύ![]() Θ°
Θ°
ΓΏ![]() Θ§Γύ
Θ§Γύ![]()
![]() Θ§ΓύΙΊ”Ύ
Θ§ΓύΙΊ”Ύ![]() ΒΡΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±
ΒΡΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±![]() ±Ί”– Β ΐΗυΘ°
±Ί”– Β ΐΗυΘ°
Θ®3Θ©ΓΏ![]() «ΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±
«ΓΑΝβœΒ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΓ±![]() ΒΡ“ΜΗωΗυΘ§Γύ
ΒΡ“ΜΗωΗυΘ§Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°
ΓΏ![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°
ΓΏΝβ–ΈΟφΜΐ «25Θ§Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§Γύ
Θ§Γύ![]() Θ°
Θ°