Question

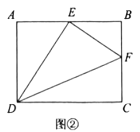
【题目】已知，在长方形中，，，点，分别是边，上的点，连接，，．

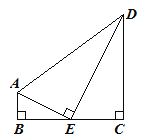
（1）如图①，当时，试说明是直角三角形；

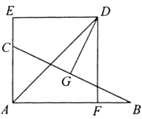
（2）如图②，若点是边的中点，平分，求的长．

Answer 1

【答案】（1）见解析；（2）．

【解析】

（1）根据，，可求出AE、BF的长，利用勾股定理可分别求出DE、EF、DF的长，根据勾股定理逆定理即可得答案；

（2）如图，作于，利用AAS可证明，可得，，根据点E为AB中点可得EB=4，即可证明EH=EB，利用HL可证明，可得BF=HF，设，可得，DF=6+x，在中，利用勾股定理列方程求出x的值即可得答案．

（1）∵，，，

∴，，BF=4，

∵四边形是长方形，

∴.

在中，，

在中，，

在中，，

∴，

∴是直角三角形，且．

（2）如图，作于，

∴，

∵平分，

∴，

在与中，，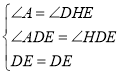

∴，

∴，，

∵点E为AB中点，

∴BE=AE=4，

∴

在与中，，

∴，

∴，

设，则，，

∴，

∴在中，，

∴，

∴，即．