题目内容
 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是
如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是
- A.

- B.

- C.

- D.

A
分析:首先求得△ABC三边的长,然后分别求得A,B,C,D各三角形的三边的长,然后根据三组对应边的比相等的两个三角形相似,即可求得答案.
解答: 解:如图:AB=
解:如图:AB=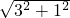 =
= ,AC=
,AC= =
= ,BC=2,
,BC=2,
A、∵DE= =
= ,DF=
,DF= =
= ,EF=1,
,EF=1,
∴ ,
,
∴△DEF∽△BAC,
故本选项正确;
B、∵MN= =
= ,MK=
,MK= =
= ,NK=3,
,NK=3,
∴ ,
, =1,
=1, ,
,
∴△MNK与△ABC不相似,
故本选项错误;
C、∵PQ= =2
=2 ,PR=
,PR= =
= ,QR=1,
,QR=1,
∴ =
= ,
, =
= ,
, =
= ,
,
∴△PQR与△ABC不相似,
故本选项错误;
D、∵GH= =
= ,GL=
,GL= =
= ,HL=2,
,HL=2,
∴ =
= ,
, =
= ,
, =
= ,
,
∴△GHL与△ABC不相似,
故本选项错误.
故选A.
点评:此题考查了相似三角形的判定.此题难度适中,注意掌握三组对应边的比相等的两个三角形相似定理的应用是解此题的关键.
分析:首先求得△ABC三边的长,然后分别求得A,B,C,D各三角形的三边的长,然后根据三组对应边的比相等的两个三角形相似,即可求得答案.
解答:
 解:如图:AB=
解:如图:AB=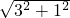 =
= ,AC=
,AC= =
= ,BC=2,
,BC=2,A、∵DE=
 =
= ,DF=
,DF= =
= ,EF=1,
,EF=1,∴
 ,
,∴△DEF∽△BAC,
故本选项正确;
B、∵MN=
 =
= ,MK=
,MK= =
= ,NK=3,
,NK=3,∴
 ,
, =1,
=1, ,
,∴△MNK与△ABC不相似,
故本选项错误;
C、∵PQ=
 =2
=2 ,PR=
,PR= =
= ,QR=1,
,QR=1,∴
 =
= ,
, =
= ,
, =
= ,
,∴△PQR与△ABC不相似,
故本选项错误;
D、∵GH=
 =
= ,GL=
,GL= =
= ,HL=2,
,HL=2,∴
 =
= ,
, =
= ,
, =
= ,
,∴△GHL与△ABC不相似,
故本选项错误.
故选A.
点评:此题考查了相似三角形的判定.此题难度适中,注意掌握三组对应边的比相等的两个三角形相似定理的应用是解此题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为
如图,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为| 5 |
| 2 |
| A、4个 | B、8个 |
| C、12个 | D、16个 |
 如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下面图中的三角形(阴影部分)与△ABC相似的是( )
 (2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( )
(2012•北塘区二模)如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为( ) 如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.
如图,小正方形的边长为1,试在图中作出2条长度不是有理数的线段和两条长度是有理数的线段.