Question

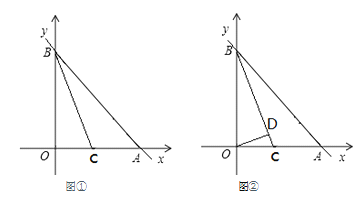
【题目】如图①，直线AB与x轴正半轴交于A（a，0）与y轴正半轴交于B（0，b）.

（1）若a+b=8，且，求△AOB的面积；

（2）若分式的值为0，过点B作BC平分∠OBA交x轴于C点，求证：;

（3）如图②,在（2）的条件下，过O点作OD⊥BC于D点,求的值.

Answer 1

【答案】（1）；（2）证明见解析；（3）2

【解析】

（1）根据对已知化简求值，可求得ab=16，然后利用三角形面积公式即可求解；

（2）由分式为0，证得, 作，根据角平分线的性质及等腰三角形的性质，可证得结论；

（3）由（2）可求得；易证得，证得得，由可求得结果.

（1）由得：

∵，∴，

∴；

（2）∵分式的值为0，

∴，∴为等腰直角三角形；

如图，作于，

∵BC平分∠OBA

∴,

∵为等腰直角三角形

∴

∴为等腰直角三角形

∴

∴

（3）如图：设，由(2)中的结论

，∴

∵，∴, ∴,即；

∵

∵

∴

∴即

∵

∴

∴即

∴

∴