Question

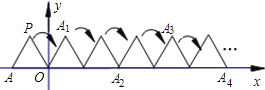
【题目】如图：将边长为1的正三角形OAP，沿x轴正方向连续翻转若干次，点A依次落在点A1，A2，A3，A4，…，A2019的位置上，则点A2019的坐标为______．

Answer 1

【答案】（3027.5，）

【解析】

作PD⊥OA于D，由题意结合图形可知，A2的横坐标为2，A4的横坐标为3+2=5，那么A6的横坐标为3+3+2=8，A2n的横坐标为3n-1，求出A2018的横坐标，然后求出A2019的横坐标，再求出PD的长，即可得出A2019的纵坐标．

解：作PD⊥OA于D，如图所示：

∵△OAP是边长为1的正三角形，

∴OD=OA=，A2的横坐标为2，A4的横坐标为3+2=5，

∴A2n的横坐标为3n-1，

∴点A2018的横坐标为3×1009-1=3026，

∴点A2019的横坐标为3026+1+0.5=3027.5，

∵PD==，

∴点P、A1、A2019的纵坐标为，

∴点A2019的坐标为（3027.5，）．

故答案为：（3027.5，）．