题目内容
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,
垂足为E,ED的延长线与AC的延长线交于点F。
(1)求证:DE是⊙O的切线;
 (2)若⊙O的半径为2,BE=1,求cosA的值.
(2)若⊙O的半径为2,BE=1,求cosA的值.
 |
解:(1)证明:连结AD、OD
∵AC是直径
∴AD⊥BC (2分)
 ∵AB=AC
∵AB=AC
∴D是BC的中点
又∵O是AC的中点
∴OD//AB (4分)
∵DE⊥AB
∴OD⊥DE
∴DE是⊙O的切线 (6分)
(2)由( 1
1 )知OD//AE
)知OD//AE
∴ (8分)
(8分)
∴
∴
解得FC=2
∴AF=6
∴cosA=

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 π C.
π C. π D.
π D. π
π
 与△COD面积之比是( )
与△COD面积之比是( )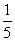 B.
B.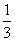

 C.
C. D.
D.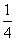

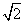 ,则平移的距离是 。
,则平移的距离是 。
 轴交于点A,与
轴交于点A,与 轴交于点B,与直线OC:
轴交于点B,与直线OC: 交于点C.
交于点C. ,
, ②求△OAC的面积.
②求△OAC的面积.  的平分线ON,若AB⊥O
的平分线ON,若AB⊥O N,垂足为E,△OAC的面积为6,
N,垂足为E,△OAC的面积为6,
 =___________。
=___________。