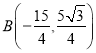题目内容
【题目】在平面直角坐标系中,一次函数![]() 图象与x轴交于点A,与y轴交于点B.
图象与x轴交于点A,与y轴交于点B.
(1)请直接写出点A坐标______,点B坐标________;
(2)点C是直线AB上一个动点,当△AOC的面积是△BOC的面积的2倍时,求点C的坐标;
(3)点D为直线AB上的一个动点,在平面内找另一个点E,且以O、B、D、E为顶点的四边形是菱形,请直接写出满足条件的菱形的周长_______.
【答案】(1)(3,0)(0,3);(2)(1,2)(-3,6);(3)12或![]() .
.
【解析】
(1)依据一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,即可得到
,即可得到![]() 点和
点和![]() 点的坐标;
点的坐标;
(2)求出![]() ,分两种情况,由面积关系可求出点
,分两种情况,由面积关系可求出点![]() 的坐标;
的坐标;
(3)分![]() 为边和为对角线两种情况,利用菱形的性质及直角三角形的性质即可得出结论.
为边和为对角线两种情况,利用菱形的性质及直角三角形的性质即可得出结论.
解:(1)在![]() 中,令
中,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
![]() ,
,![]() ;
;
故答案为:![]() ;
;![]() .
.
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
①当点![]() 在线段
在线段![]() 上时,如图1,
上时,如图1,
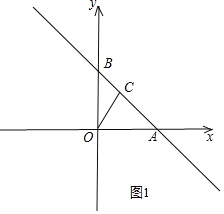
![]() 的面积是
的面积是![]() 的面积的2倍,
的面积的2倍,
![]() ,
,
![]()
![]()
![]() 或
或![]() (舍去),
(舍去),
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
![]() .
.
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,
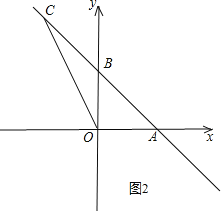
![]() 的面积是
的面积是![]() 的面积的2倍,
的面积的2倍,
![]() ,
,
![]()
![]() ,
,
![]() 或
或![]() (舍去),
(舍去),
![]() .
.
综合以上可得点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
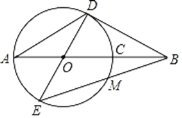
(3)如图3,以![]() 为边的菱形
为边的菱形![]() 中,
中,
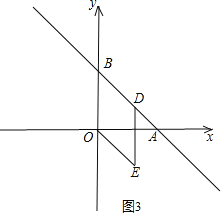
![]() ,
,
![]() 周长为
周长为![]() ,
,
如图4,以![]() 边的菱形
边的菱形![]() 中,同理周长为12.
中,同理周长为12.

如图5,以![]() 为对角线的菱形
为对角线的菱形![]() 中,
中,
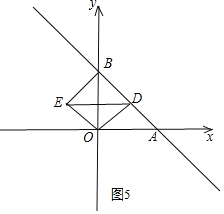
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() .
.
![]() 四边形
四边形![]() 的周长为
的周长为![]() .
.
综上可得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的菱形的周长为12或
为顶点的菱形的周长为12或![]() .
.
故答案为:12或![]() .
.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目