题目内容
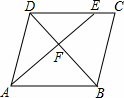
已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．
（1）如图1，连接BD，AF，则BD AF（填“＞”、“＜”或“=”）；
（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．
（1）解：由AB=AC，
得∠ABC=ACB．
由△ABC沿BC方向平移得到△DEF，
得DF=AC，∠DFE=∠ACB．
在△ABF和△DBF中，
，
△ABF≌△DBF（SAS），
BD=AF，
故答案为：BD=AF；
（2）证明：如图：
，
MN∥BF，
△AMG∽△ABC，△DHN∽△DEF，
=
，
，
∴MG=HN，MB=NF．
在△BMH和△FNG中，
，
△BMH≌△FNG（SAS），
∴BH=FG．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
有意义的x的取值范围是 
的解集是 
