题目内容
 如图,在⊙O中,弦AB的长为10,圆周角∠ACB=45°,则这个圆的直径AD为
如图,在⊙O中,弦AB的长为10,圆周角∠ACB=45°,则这个圆的直径AD为
- A.

- B.
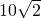
- C.

- D.
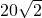
B
分析:连接BD,由∠ACB=45°,即可推出∠ADB=45°,再由直径AD,推出∠ABD=90°后,根据直角三角形的性质即可推出AD的长度.
解答:连接BD,
∵∠ACB=45°,
∴∠ADB=45°,
∵直径AD,
∴∠ABD=90°,
∵AB=10,
∴AD=10 .
.
故选B.

点评:本题主要考查直角三角形的性质,圆周角定理等知识点,关键在于正确的做出辅助线,根据图形推出∠ADB=45°,∠ABD=90°.
分析:连接BD,由∠ACB=45°,即可推出∠ADB=45°,再由直径AD,推出∠ABD=90°后,根据直角三角形的性质即可推出AD的长度.
解答:连接BD,
∵∠ACB=45°,
∴∠ADB=45°,
∵直径AD,
∴∠ABD=90°,
∵AB=10,
∴AD=10
 .
.故选B.

点评:本题主要考查直角三角形的性质,圆周角定理等知识点,关键在于正确的做出辅助线,根据图形推出∠ADB=45°,∠ABD=90°.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
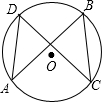 已知:如图,在⊙O中,弦AD=BC.求证:AB=CD.
已知:如图,在⊙O中,弦AD=BC.求证:AB=CD. 4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( ) 标系.
标系. 如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( )
如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( ) 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.