题目内容
【题目】如图,直线l:y=x﹣![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:_____;
(2)已知点Q是抛物线y=![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
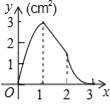
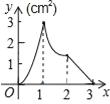
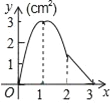
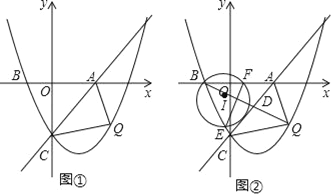
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
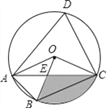
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
【答案】(1)![]() (2)①
(2)①![]() ,
, ![]()
![]() ,②
,②![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
【解析】试题分析:(1)令![]() ,求出直线
,求出直线![]() 与y轴的交点即C点坐标,再用待定系数法求二次函数解析式即可;(2)①在直线
与y轴的交点即C点坐标,再用待定系数法求二次函数解析式即可;(2)①在直线![]() 中,令
中,令![]() ,得到点A的坐标,连接
,得到点A的坐标,连接![]() ,由
,由![]() 即可得到
即可得到![]() 与
与![]() 的函数关系;②由点
的函数关系;②由点![]() 得
得![]() . 作直径
. 作直径![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ,当
,当![]() 时,此时直径
时,此时直径![]() 最小,即直径
最小,即直径![]() 最小,
最小, ![]() 的值最小.
的值最小. ![]() ,
, ![]() =
= ![]() =
=![]() ,
,
求出点![]() 的坐标.
的坐标.
试题解析:(1)在直线![]() 中,令
中,令![]() ,则
,则![]() ,∴点
,∴点![]()
把点![]() 与点
与点![]() 代入
代入![]() ,得:
,得:  ,解得:
,解得: 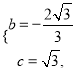 ,
,
∴抛物线的解析式为: ![]() .
.
(2) ①连接![]() ,在直线
,在直线![]() 中,令
中,令![]() ,则
,则![]() ,
,

∴点![]() .
.
∵![]() ,
,
∴ ,
,
∴![]() ,
,
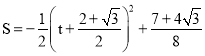 ,
, ![]() .
.
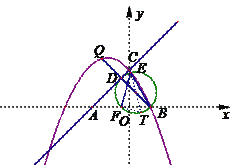
∴当![]() 时,
时, ![]() .
.
②∵![]() ∴
∴![]() ,
, ![]() .
.
在![]() 中,
中, ![]()
∴![]() .
.
作直径![]() 交⊙
交⊙![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() ,
, ![]() ,
,
![]() ,
,
当![]() 时,此时直径
时,此时直径![]() 最小,即直径
最小,即直径![]() 最小,
最小, ![]() 的值最小.
的值最小.
![]() ,
,
∴![]() ,
,
![]()
∴![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目