题目内容
 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
证明:(1)BF=DF;(2)AE∥BD.
证明:(1)由折叠的性质知,CD=ED,BE=BC.
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠BAD=90°,
∴AB=DE,BE=AD,BD=BD,
∴△ABD≌△EDB,
∴∠EBD=∠ADB,
∴FB=FD;
(2)∵AD=BE,AB=DE,AE=AE,
∴△AED≌△EAB(SSS),
∴∠AEB=∠EAD,
∵∠AFE=∠BFD,
∴∠AEB=∠EBD,
∴AE∥BD.
分析:(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;
(2)易得△AED≌△EAB.那么∠AEB=∠EAD.所以AF=EF,∵∠AEF=(180°-∠AFE)÷2=(180°-∠BFD)÷2=∠FBD,∴AE∥BD.
点评:本题利用了:
①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
②全等三角形的判定和性质,等角对等边,三角形的内角和,平行线的判定求解.
∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠BAD=90°,
∴AB=DE,BE=AD,BD=BD,
∴△ABD≌△EDB,

∴∠EBD=∠ADB,
∴FB=FD;
(2)∵AD=BE,AB=DE,AE=AE,
∴△AED≌△EAB(SSS),
∴∠AEB=∠EAD,
∵∠AFE=∠BFD,
∴∠AEB=∠EBD,
∴AE∥BD.
分析:(1)由折叠的性质可得到△ABD≌△EDB,那么∠ADB=∠EBD,所以BF=DF;
(2)易得△AED≌△EAB.那么∠AEB=∠EAD.所以AF=EF,∵∠AEF=(180°-∠AFE)÷2=(180°-∠BFD)÷2=∠FBD,∴AE∥BD.
点评:本题利用了:
①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;
②全等三角形的判定和性质,等角对等边,三角形的内角和,平行线的判定求解.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
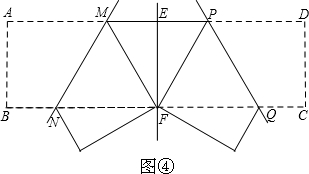
 23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
23、如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.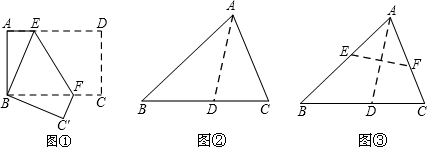
 (2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( )
(2013•松北区三模)如图,将矩形纸片ABCD折痕,使点D落在点线段AB的中点F处.若AB=4,则边BC的长为( ) 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
