Question

等边三角形的外接圆面积是内切圆面积的

1. A.
   3倍
2. B.
   5倍
3. C.
   4倍
4. D.
   2倍

Answer 1

C
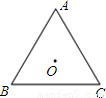
分析：根据题意画出图形，设O是等边三角形ABC的内心，连接OB，OA，延长AO交BC于D，根据等边三角形的性质得出O也是△ABC的外心，∠OBD=30°，AD⊥BC，推出OB=2OD，分别求出等边三角形ABC的外接圆、内切圆的面积，即可求出答案．
解答：
设O是等边三角形ABC的内心，连接OB，OA，延长AO交BC于D，
∵三角形ABC是等边三角形，
∴O也是△ABC的外心，∠OBD=∠ABC=30°，AD⊥BC，
∴OB=2OD，
∵等边三角形ABC的外接圆的面积是π×OB²=π（2OD）²=4πOD²，
等边三角形ABC的内切圆的面积是π×OD²，
∴等边三角形ABC的外接圆面积是内切圆面积的4倍，
故选C．
点评：本题考查了等边三角形的性质，三角形的内切圆与外接圆，含30度角的直角三角形性质等知识点的应用，关键是求出OB=2OD，主要考查了学生的计算能力，题型较好，难度也适中．