题目内容
如图,在直角坐标系xOy中,点A(m,0)(其中m<0)、点B(4,0)、C(4,m),D(m,-4).点E是y轴正半轴上的一点,且 0E=AB.分别连接AE,DE,CE 和BE
(1)求点E的坐标(用含 m的式子表示);
(2)若m=-1.2时,连接CD,求S△CDE;
(3)当点A在x 轴的负半轴上运动时, 的值是否发生变化?若改变,请说明理由;若不变,请求出其值.
的值是否发生变化?若改变,请说明理由;若不变,请求出其值.

解:(1)∵A(m,0)(其中m<0)、B(4,0),
∴OA=-m,OB=4,
∴AB=4-m.
∵0E=AB,
∴OE=4-m,
∴E(0,4-m).
答:点E的坐标为(0,4-m);
(2)当m=-1.2时,
∴OE=4-(-1.2)=5.2,AB=5.2
∵B(4,0)、C(4,m),D(m,-4),AB⊥x轴,CB⊥x轴,
∴AD=4,CB=1.2.OA=1.2,OB=4
∵S△EDC=S梯形ADCB+S△EAB-S△AED-S△EBC,
∴S△EDC= +
+ -
- -
- ,
,
=22.24.
答:S△EDC=22.24;
(3) 的值是不变.
的值是不变.
理由:连接AC、BD.
∵AB⊥x轴,CB⊥x轴,
∴∠ABC=∠BAD=90°.
∵∠AOE=∠BOE=90°,
∴∠AOE=∠CBA,∠BOE=∠DAB.
∵A(m,0)(其中m<0)、点B(4,0)、C(4,m),D(m,-4),
∴OA=-m,BC=-m,AD=4,OB=4,
∴OA=BC,OB=AD.
在△AOE和△CBA中 ,
,
 ,
,
∴△AOE≌△CBA(SAS),
∴∠AEO=∠CAB,AE=AC.
∵∠AEO+∠EAO=90°,
∴∠CAB+∠EAO=90°,
即∠CAE=90°,
∴△CAE是等腰直角三角形,
∴∠AEC=45°.
在△OBE和ADB中,
 ,
,
∴△OBE≌ADB(SAS),
∴∠BEO=∠DBA,BE=BD,
∵∠BEO+∠OBE=90°,
∴∠DBA+∠OBE=90°,
即∠DBE=90°,
∴△DBE是等腰直角三角形,
∴∠DEB=45°,
∴∠AEC=∠DEB,
∴∠AEC-∠DEC=∠DEB-∠DEC,
∴∠AED=∠BEC,
∴ =1.
=1.
分析:(1)根据A、B的坐标,求出AB的值,就可以表示出OE,从而求出E的坐标;
(2)当m=-1.2时,代入E的坐标,求出OE,由S△EDC=S梯形ADCB+S△EAB-S△AED-S△EBC就可以求出结论;
(3)连接AC、BD,根据条件可以得出△AOE≌△CBA,△OBE≌ADB,根据全等三角形的性质可以得出∠AED=∠BEC,从而得出结论.
点评:本题考查了坐标与图形的性质的运用,三角形的面积公式的运用,等腰直角三角形的判定及性质的运用,全等三角形的判定与性质的运用,解答时运用三角形全等的性质求解是关键.
∴OA=-m,OB=4,
∴AB=4-m.
∵0E=AB,
∴OE=4-m,
∴E(0,4-m).
答:点E的坐标为(0,4-m);
(2)当m=-1.2时,
∴OE=4-(-1.2)=5.2,AB=5.2
∵B(4,0)、C(4,m),D(m,-4),AB⊥x轴,CB⊥x轴,
∴AD=4,CB=1.2.OA=1.2,OB=4
∵S△EDC=S梯形ADCB+S△EAB-S△AED-S△EBC,
∴S△EDC=
 +
+ -
- -
- ,
,=22.24.
答:S△EDC=22.24;
(3)
 的值是不变.
的值是不变.理由:连接AC、BD.
∵AB⊥x轴,CB⊥x轴,
∴∠ABC=∠BAD=90°.
∵∠AOE=∠BOE=90°,
∴∠AOE=∠CBA,∠BOE=∠DAB.
∵A(m,0)(其中m<0)、点B(4,0)、C(4,m),D(m,-4),
∴OA=-m,BC=-m,AD=4,OB=4,
∴OA=BC,OB=AD.
在△AOE和△CBA中
 ,
, ,
,∴△AOE≌△CBA(SAS),
∴∠AEO=∠CAB,AE=AC.
∵∠AEO+∠EAO=90°,
∴∠CAB+∠EAO=90°,
即∠CAE=90°,
∴△CAE是等腰直角三角形,
∴∠AEC=45°.
在△OBE和ADB中,
 ,
,∴△OBE≌ADB(SAS),
∴∠BEO=∠DBA,BE=BD,
∵∠BEO+∠OBE=90°,
∴∠DBA+∠OBE=90°,
即∠DBE=90°,
∴△DBE是等腰直角三角形,
∴∠DEB=45°,
∴∠AEC=∠DEB,
∴∠AEC-∠DEC=∠DEB-∠DEC,
∴∠AED=∠BEC,
∴
 =1.
=1.分析:(1)根据A、B的坐标,求出AB的值,就可以表示出OE,从而求出E的坐标;
(2)当m=-1.2时,代入E的坐标,求出OE,由S△EDC=S梯形ADCB+S△EAB-S△AED-S△EBC就可以求出结论;
(3)连接AC、BD,根据条件可以得出△AOE≌△CBA,△OBE≌ADB,根据全等三角形的性质可以得出∠AED=∠BEC,从而得出结论.
点评:本题考查了坐标与图形的性质的运用,三角形的面积公式的运用,等腰直角三角形的判定及性质的运用,全等三角形的判定与性质的运用,解答时运用三角形全等的性质求解是关键.

练习册系列答案
相关题目
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.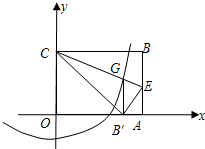 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标. 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D. 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.