题目内容
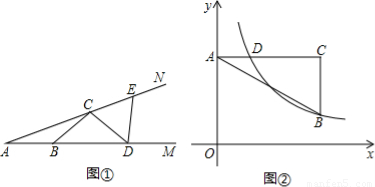
(1)先求解下列两题:①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.

【答案】
(1)①∠A=21②k=3(2)见解析
【解析】解:(1)①∵AB=BC=CD=DE,
∴∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,
根据三角形的外角性质,∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,
又∵∠EDM=84°,
∴∠A+3∠A=84°,解得,∠A=21°。
②∵点B在反比例函数 图象上,点B,C的横坐标都是3,∴点B(3,
图象上,点B,C的横坐标都是3,∴点B(3, )。
)。
∵BC=3,∴点C(3, +2)。
+2)。
∵AC∥x轴,点D在AC上,且横坐标为1,∴A(1, +2)。
+2)。
∵点A也在反比例函数图象上,∴ +2=k。解得,k=3。
+2=k。解得,k=3。
(2)用已知的量通过关系去表达未知的量,使用转换的思维和方法,转换为解一元一次方程。
(1)①根据等边对等角可得∠A=∠BCA,∠CBD=∠BDC,∠ECD=∠CED,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠BCA=∠CBD,∠A+∠CDB=∠ECD,∠A+∠CED=∠EDM,然后用∠A表示出∠EDM,计算即可求解。
②先根据反比例函数图象上的点的坐标特征表示出点B的坐标,再表示出点C的坐标,然后根据AC∥x轴可得点C、D的纵坐标相同,从而表示出点D的坐标,再代入反比例函数解析式进行计算即可得解.
(2)从数学思想上考虑解答。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.
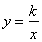
 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.