ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓБпЃЉНЛ
ЕФзѓБпЃЉНЛ![]() жсе§АыжсгкЕу
жсе§АыжсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЖЅЕу.
ЮЊХзЮяЯпЖЅЕу.
ЃЈ1ЃЉжБНгаДГі![]() Ш§ЕуЕФзјБъМА
Ш§ЕуЕФзјБъМА![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕу![]() ЮЊХзЮяЯпдк
ЮЊХзЮяЯпдк![]() жсЩЯЗНЕФвЛЕуЃЌЧв
жсЩЯЗНЕФвЛЕуЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌ![]() ЮЊ
ЮЊ![]() ЕФЭтаФЃЌЕу
ЕФЭтаФЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ДгЕу
ЗжБ№ДгЕу![]() ЭЌЪБГіЗЂвд2ЕЅЮЛ/
ЭЌЪБГіЗЂвд2ЕЅЮЛ/![]() ЃЌ1ЕЅЮЛ/
ЃЌ1ЕЅЮЛ/![]() ЫйЖШбиЩфЯп
ЫйЖШбиЩфЯп![]() ЃЌ
ЃЌ![]() зїдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊ
зїдШЫйдЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() УыЃЈ
УыЃЈ![]() Чв
Чв![]() ЃЉЃЌжБЯп
ЃЉЃЌжБЯп![]() НЛгк
НЛгк![]() .
.
ЂйЧѓжЄЃКЕу![]() дкЖЈжБЯп
дкЖЈжБЯп![]() ЩЯВЂЧѓ
ЩЯВЂЧѓ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЂкШє![]() дкХзЮяЯпЩЯЧвдкжБЯп
дкХзЮяЯпЩЯЧвдкжБЯп![]() ЯТЗНЃЌЕБ
ЯТЗНЃЌЕБ![]() ЕНжБЯп
ЕНжБЯп![]() ОрРызюДѓЪБЃЌЧѓЕу
ОрРызюДѓЪБЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() ЃЌМћНтЮіЃЌЂк
ЃЌМћНтЮіЃЌЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋy=0ЃЌx=0ДњШыМДПЩаДГі![]() Ш§ЕуЕФзјБъМА
Ш§ЕуЕФзјБъМА![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЯШЧѓ![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌСЊСЂ
ЃЌСЊСЂ![]() НтЕУЃК
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() .
.
ЃЈ3ЃЉЂйЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩ
ЃЌПЩ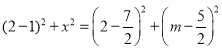 НтЕУЃК
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ПЩЕУ
ПЩЕУ![]() ЕБ
ЕБ![]() ЪБЃЌЭЌРэПЩЧѓ
ЪБЃЌЭЌРэПЩЧѓ![]() ЃЌЙЪ
ЃЌЙЪ![]() дкжБЯп
дкжБЯп![]() ЩЯ.
ЩЯ.
ЂкЕБ![]() ЕН
ЕН![]() ОрРызюДѓЪБЃЌЩшЙ§
ОрРызюДѓЪБЃЌЩшЙ§![]() Чвгы
Чвгы![]() ЦНааЕФжБЯпЕФНтЮіЪНЮЊЃК
ЦНааЕФжБЯпЕФНтЮіЪНЮЊЃК ![]() СЊСЂ
СЊСЂ![]() РћгУИУЗНГЬзщгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌПЩЕУЗНГЬ
РћгУИУЗНГЬзщгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌПЩЕУЗНГЬ![]() гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЧѓЕУ
гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЧѓЕУ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌПЩЕУЕу
ЃЌПЩЕУЕу![]() ЕФзјБъ.
ЕФзјБъ.
ЃЈ1ЃЉЁпХзЮяЯп![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЖЅЕу.
ЮЊХзЮяЯпЖЅЕу.
Ёр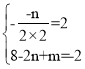
НтЕУ![]()
Ёр![]()
ЕБy=0ЪБЃЌ![]()
НтЕУ![]()
Ёр![]()
ЕБx=0ЪБЃЌ![]()
НтЕУ![]()
Ёр![]()
Ёр![]()
ЃЈ2ЃЉЁп![]()
Ёр![]()
Щш![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]()
гжвђЮЊAЃЈ1ЃЌ0ЃЉ.ДњШы![]() НтЕУЃКb=-1
НтЕУЃКb=-1
ЙЪ![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
Ёр![]()
НтЕУЃК![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
ЃЈ3ЃЉЂйЩш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
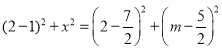
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌЭЌРэПЩЧѓ
ЪБЃЌЭЌРэПЩЧѓ![]() ЃЌЙЪ
ЃЌЙЪ![]() дкжБЯп
дкжБЯп![]() ЩЯ.
ЩЯ.
ЂкЕБ![]() ЕН
ЕН![]() ОрРызюДѓЪБЃЌЩшЙ§
ОрРызюДѓЪБЃЌЩшЙ§![]() Чвгы
Чвгы![]() ЦНааЕФжБЯпЕФНтЮіЪНЮЊЃК
ЦНааЕФжБЯпЕФНтЮіЪНЮЊЃК
![]()
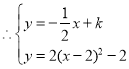 гаСНЕШИљ
гаСНЕШИљ
![]() гаЕШИљЃЌ
гаЕШИљЃЌ![]()
![]()