Question

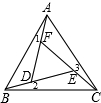如图，等边△ABC中，∠1=∠2=∠3，（1）求证：DE=EF=DF；（2）求∠BEC的度数．

Answer 1

解：（1）∵△ABC是等边三角形，
∴∠BAC=∠ABC=∠ACB=60°，
∴AB=BC=AC，
又∵∠1=∠2=∠3，
∴∠CAF=∠ABD=∠ECB，
∴△ADB≌△BEC≌△CFA，
∴EF=DE=DF；

（2）由（1）可知△DEF为等边三角形，
∴∠DFE=∠DEF=∠EDF=60°，
∵∠BEC=∠FDE+∠EFD，
∴∠BEC=120°．
分析：（1）根据等边三角形的性质，再根据全等三角形的判定即可证明△ADB≌△BEC≌△CFA，再根据全等三角形的性质即可得出EF=DE=DF，
（2）由（1）可知△DEF为等边三角形，根据等边三角形的性质以及三角形的外角性质即可得出答案．
点评：本题主要考查了等边三角形的性质，全等三角形的判定及性质以及三角形的外角性质，难度适中．