题目内容
一次函数y=(k- )x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求k的值;
(2)若一抛物线经过点A、B、C三点,求此抛物线的解析式。
(3)当抛物线开口向上时过A、B、C三点作△ABC,求tan∠ABC的值。
解(1)⑴由题意得: ,
,
解得 <k<
<k< ,又k为偶数,∴k=2 分
,又k为偶数,∴k=2 分
⑵求得A(-3,0)、B(0,4),
∴OB=4,
 ∵S
∵S =
= ·OB·OC==2·OC=2,
·OB·OC==2·OC=2,
∴OC=1
∴C(1,0)或(-1,0)
若取C(1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x-1),
将B(0,4)代入,求得a=- .
.
∴抛物线为
若取C(-1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x+1),将B(0,4)代入,
求得a=
∴抛物线为y= x+
x+ x+4
x+4
⑶如图,过C作CD⊥AB于D,则tan∠ABC=
∵ Sin∠BAO= =
= ,cos∠BAO=
,cos∠BAO= =
=
∴  =
= , DC=
, DC= ,
, =
= ,AD=
,AD= ,
,
∴BD=
∴tan∠ABC=

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


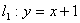 与直线
与直线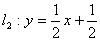 相交于点
相交于点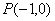 .直线
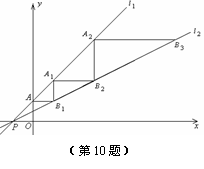
.直线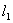 与y轴交于点A.一动点
与y轴交于点A.一动点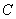 从点A出发,先沿平行于x轴的方向运动,到达直线
从点A出发,先沿平行于x轴的方向运动,到达直线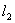 上的点
上的点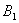 处后,改为垂直于x轴的方向运动,到达直线
处后,改为垂直于x轴的方向运动,到达直线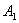 处后,再沿平行于x轴的方向运动,到达直线
处后,再沿平行于x轴的方向运动,到达直线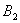 处后,又改为垂直于x轴的方向运动,到达直线
处后,又改为垂直于x轴的方向运动,到达直线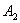 处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点
处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点 ,
, ,…,
,…,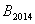 ,
,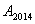 ,…
,… B.
B.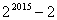 C.
C.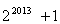 D.
D.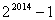

 ,若△DEF的周长为偶数,则 DF的取值为 ( )
,若△DEF的周长为偶数,则 DF的取值为 ( ) 5 (D). 3或4或5
5 (D). 3或4或5 B、
B、
 D、
D、 

 BD相交于点N,那么
BD相交于点N,那么 ( )
( ) B、
B、 C、
C、 D、
D、 
