题目内容
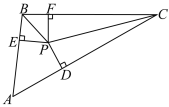
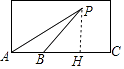
【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
【答案】解:作PH⊥BC于H.
在Rt△PBH中,∵cos∠PBH= ![]() =
= ![]() ,设BH=3k,PB=5k,则PH=4k,
,设BH=3k,PB=5k,则PH=4k,
∵∠PAB+∠PBC=90°,∠PBC+∠BPH=90°,
∴∠BPH=∠PAH,∵∠PHB=∠PHA,
∴△PBH∽△APH,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AH= ![]() k,
k,
∴AB=AH﹣BH= ![]() k﹣3k=
k﹣3k= ![]() ,
,
在Rt△APH中,∵AP=20×1=20,
∴(4k)2+( ![]() k)2=202,
k)2=202,
∴k=3,
∴AB=7,PB=15,
∴乙从A到B的运动时间= ![]() =2s,从B到P的运动时间=22﹣2=20s,
=2s,从B到P的运动时间=22﹣2=20s,
∴乙的游泳速度为 ![]() =0.75米/秒.
=0.75米/秒.
【解析】作PH⊥BC于H.在Rt△PBH中,由cos∠PBH= ![]() =
= ![]() ,设BH=3k,PB=5k,则PH=4k,由△PBH∽△APH,推出
,设BH=3k,PB=5k,则PH=4k,由△PBH∽△APH,推出 ![]() =
= ![]() ,可得AH=
,可得AH= ![]() k,AB=AH﹣BH=
k,AB=AH﹣BH= ![]() k﹣3k=
k﹣3k= ![]() ,在Rt△APH中,AP=20×1=20,利用勾股定理可得(4k)2+(
,在Rt△APH中,AP=20×1=20,利用勾股定理可得(4k)2+( ![]() k)2=202,求出k即可解决问题.
k)2=202,求出k即可解决问题.
【考点精析】利用余角和补角的特征对题目进行判断即可得到答案,需要熟知互余、互补是指两个角的数量关系,与两个角的位置无关.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目