题目内容
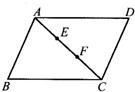 23、如图所示,在四边形ABCD中,AB∥CD,AD∥BC,点E,F在对角线AC上,且AE=CF,请你分别以E,F为一端点,和图中已标字母的某点连成两条相等的新线段(只需证明一组线段相等即可).
23、如图所示,在四边形ABCD中,AB∥CD,AD∥BC,点E,F在对角线AC上,且AE=CF,请你分别以E,F为一端点,和图中已标字母的某点连成两条相等的新线段(只需证明一组线段相等即可).(1)连接
BE,DF
;(2)结论:
BE
=DF
;(3)证明:
分析:此题的答案不唯一.可以连接BE,DF或连接BF,DE..根据平行四边形的性质和已知条件证明全等三角形,从而证明BE=DF或BF=DE.
解答:解:连接BE,DF.,
∵在四边形ABCD中,AB∥CD,AD∥BC,
∴AB=CD,∠ABE=∠CDF.,
又AE=CF.,
∴△ABE≌△CDF.
∴BE=DF.
∵在四边形ABCD中,AB∥CD,AD∥BC,
∴AB=CD,∠ABE=∠CDF.,
又AE=CF.,
∴△ABE≌△CDF.
∴BE=DF.
点评:此题是一道开放性试题.能够根据平行四边形是中心对称图形,发现怎样连接所得的两条线段一定相等.

练习册系列答案
相关题目
 22、如图所示,在四边形ABCD中,已知:AB:BC:CD:DA=2:2:3:1,且∠B=90°,求∠DAB的度数.
22、如图所示,在四边形ABCD中,已知:AB:BC:CD:DA=2:2:3:1,且∠B=90°,求∠DAB的度数. 11、如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为
11、如图所示,在四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,∠BAC=35°,则∠BCD的度数为 如图所示,在四边形ABCD中,∠BAD=90°,∠B=75°,∠ADC=135°,AB=AD=
如图所示,在四边形ABCD中,∠BAD=90°,∠B=75°,∠ADC=135°,AB=AD= 9、如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
9、如图所示,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( ) 如图所示,在四边形ABCD中,∠A=90°,AB=9,BC=20,CD=25,AD=12,求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠A=90°,AB=9,BC=20,CD=25,AD=12,求四边形ABCD的面积.