Question

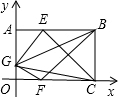
如图，已知OABC是一个长方形，其中顶点A，B的坐标分别为（0，a）和（9，a），点E在AB上，且AE=AG，点F在OC上，且OF=OC，点G在OA上，且使△GEC的面积为20，△GFB的面积为16，试求a的值．

Answer 1

解：设G之坐标为（0，b），b＞0，
∵S_{长方形OABC}-S_△GEC=S_△OGC+S_△AGE+S_△BEC
∴9a-20=•9b+•3（a-b）+•6a
解得b=a-
同理，∵S_{长方形OABC}-S_△GFB=S_△ABG+S_△OGF+S_△BFC
∴9a-16=•9（a-b）+•3b+•6a，
化简得3a=32-6b
将b=a-代入上式得
3a=72-9a，解得a=6．
分析：设G之坐标为（0，b），b＞0，根据S_{长方形OABC}-S_△GEC=S_△OGC+S_△AGE+S_△BEC和S_{长方形OABC}-S_△GFB=S_△ABG+S_△OGF+S_△BFC求得a、b的关系式，解得a、b即可解题．
点评：本题考查了矩形面积的计算，考查了三角形面积的计算，考查了二元一次方程组的求解，本题中求出关于a、b的关系式并求得a、b的值是解题的关键．