题目内容
如图，把正方形ACFG与Rt△ACB按如图（甲）所示重叠在一起，其中AC=2，∠BAC=60°，若把Rt△ACB绕直角顶点C按顺时针方向旋转，△ACB至少旋转________ 度使斜边恰好经过正方形ACFG的顶点F（如图乙）．
30
分析：根据旋转前后对应角相等可得出∠B'A'C=60°，△A'CF是等边三角形，继而可得出旋转角度∠ACA'的度数．
解答：如图所示：
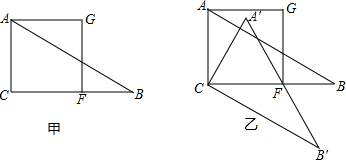
∵∠BAC=60°，四边形ACFG是正方形，
∴∠B'A'C=60°，A'C=AC=CF，
∴△A'CF是等边三角形，
∴∠A'CF=60°，∠ACA'=90°-∠A'CF=30°，
即△ACB至少旋转30°使斜边恰好经过正方形ACFG的顶点F．
故答案为：30．
点评：此题考查了正方形的性质、旋转的性质及等边三角形的判定与性质，解答本题的关键是掌握正方形的四边相等及旋转前后对应边、对应角分别相等，难度一般．
分析：根据旋转前后对应角相等可得出∠B'A'C=60°，△A'CF是等边三角形，继而可得出旋转角度∠ACA'的度数．
解答：如图所示：
∵∠BAC=60°，四边形ACFG是正方形，
∴∠B'A'C=60°，A'C=AC=CF，
∴△A'CF是等边三角形，
∴∠A'CF=60°，∠ACA'=90°-∠A'CF=30°，
即△ACB至少旋转30°使斜边恰好经过正方形ACFG的顶点F．
故答案为：30．
点评：此题考查了正方形的性质、旋转的性质及等边三角形的判定与性质，解答本题的关键是掌握正方形的四边相等及旋转前后对应边、对应角分别相等，难度一般．
练习册系列答案
相关题目
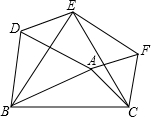（2013•南安市质检）如图，已知△ABC，点A在BC边的上方，把△ABC绕点B逆时针方向旋转60°得△DBE，绕点C顺时针方向旋转60°得△FEC，连结AD、AF．