��Ŀ����
����ǡ�ABC�У�AB=4��BC=5����ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1��
��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1A1�Ķ�����
��2����ͼ2������AA1��CC1������ABA1�����Ϊ4�����CBC1�������
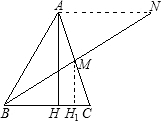
��3����ͼ3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1�����߶�EP1���ȵ����ֵ����Сֵ��

���㣺���������ε��ж������ʣ�ȫ�������ε��ж������ʣ���ת�����ʡ�
��𣺽⣺��1������ת�����ʿɵã���A1C1B=��ACB=45�㣬BC=BC1��
���CC1B=��C1CB=45�㣬..����2�֣�
���CC1A1=��CC1B+��A1C1B=45��+45��=90�㣮����3�֣�
��2���ߡ�ABC�ա�A1BC1��
��BA=BA1��BC=BC1����ABC=��A1BC1��
��![]() ����ABC+��ABC1=��A1BC1+��ABC1��
����ABC+��ABC1=��A1BC1+��ABC1��
���ABA1=��CBC1��
���ABA1�ס�CBC1������5�֣�
�� ��
��
��S��ABA1=4��
��S��CBC1=![]() ������7�֣�
������7�֣�
��3������B��BD��AC��DΪ���㣬
�ߡ�ABCΪ��������Σ�
���D���߶�AC�ϣ�
��Rt��BCD�У�BD=BC��sin45��=![]() ������8�֣�
������8�֣�
����ͼ1����P��AC���˶��������D����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB��ʱ��EP1��С����СֵΪ��EP1=BP1��BE=BD��BE=![]() ��2������9�֣�
��2������9�֣�
�ڵ�P��AC���˶�����C����ABC�Ƶ�B��ת��ʹ��P�Ķ�Ӧ��P1���߶�AB���ӳ�����ʱ��EP1������ֵΪ��EP1=BC+AE=2+5=7������10�֣�



 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�| A��a��b��c | ||||||
B��
| ||||||
| C��cosA��cosB��cosC | ||||||
| D��sinA��sinB��sinC |
 ����ǡ�ABC�У����ĸ���AH��������BM����֤����B��60�㣨��ͼ����
����ǡ�ABC�У����ĸ���AH��������BM����֤����B��60�㣨��ͼ���� ��ͼ������ǡ�ABC�У���BAC=60�㣬BD��CEΪ�ߣ�FΪBC���е㣬����DE��DF��EF������ۣ���B��E��D��C�ĵ㹲Բ����AD•AC=AE•AB���ۡ�DEF�ǵȱ������Σ��ܵ���ABC=45��ʱ��BE=
��ͼ������ǡ�ABC�У���BAC=60�㣬BD��CEΪ�ߣ�FΪBC���е㣬����DE��DF��EF������ۣ���B��E��D��C�ĵ㹲Բ����AD•AC=AE•AB���ۡ�DEF�ǵȱ������Σ��ܵ���ABC=45��ʱ��BE= ��2013•�Ͽ���һģ������ǡ�ABC�У���BAC=60�㣬BD��CEΪ�ߣ�F��BC���е㣬����DE��EF��FD�������½�����һ����ȷ�ĸ����У�������
��2013•�Ͽ���һģ������ǡ�ABC�У���BAC=60�㣬BD��CEΪ�ߣ�F��BC���е㣬����DE��EF��FD�������½�����һ����ȷ�ĸ����У�������