题目内容
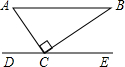如图，一直角三角形硬纸板ABC的直角顶点C放在直线DE上，使AB∥DE，若∠BCE=35°，则∠A的度数为
- A.35°
- B.45°
- C.55°
- D.65°
C
分析：根据平行线的性质，求出∠B的值，再根据三角形的内角和定理，求出∠A的值．
解答：∵AB∥DE，
∴∠B=∠BCE=35°，
∴∠A=180°-90°-35°=55°．
故选C．
点评：此题考查的是平行线的性质及三角形的内角和定理，关键是求出∠B的度数．
分析：根据平行线的性质，求出∠B的值，再根据三角形的内角和定理，求出∠A的值．
解答：∵AB∥DE，
∴∠B=∠BCE=35°，
∴∠A=180°-90°-35°=55°．
故选C．
点评：此题考查的是平行线的性质及三角形的内角和定理，关键是求出∠B的度数．
练习册系列答案
相关题目
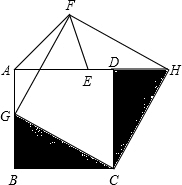探索．先在BA上选取点G，使BG=b，连接CG，剪下△BCG并绕点C顺时针旋转90°到△CDH的位置，接下来的问题是：
（2013•泰州一模）一个包装盒的设计方法如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=xcm．若广告商要求包装盒侧面积S（cm2）最大，试问x应取的值为
已知：如图，小明把一张直角三角形的硬纸片像图中那样折叠，使得A与B重合，小明看到硬纸片上标着AB=20cm，请你猜猜CE的长是