题目内容
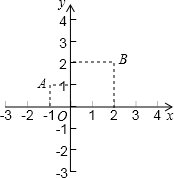 在平面直角坐标系xOy中,二次函数y=-
在平面直角坐标系xOy中,二次函数y=-| 1 |
| 3 |
(1)b=
| 2 |
| 3 |
| 2 |
| 3 |
2
2
;对称轴是直线x=1
x=1
;(2)如果点P在直线AB上,且△POB与△BCD相似,求点P的坐标.
分析:(1)利用待定系数法求出二次函数解析式即可;
(2)先利用直线OA的表达式y=-x,得出点C的坐标为(1,-1),则AB=BC,OA=OC,再根据等腰三角形三线合一的性质得出∠ABO=∠CBO.然后分两种情况进行讨论:①∠BOP=∠BDC,②∠BOP=∠BCD,进而分析得出P点坐标即可.
(2)先利用直线OA的表达式y=-x,得出点C的坐标为(1,-1),则AB=BC,OA=OC,再根据等腰三角形三线合一的性质得出∠ABO=∠CBO.然后分两种情况进行讨论:①∠BOP=∠BDC,②∠BOP=∠BCD,进而分析得出P点坐标即可.
解答:解:(1)根据题意得:
,
解得:
,
则所求的二次函数的解析式是:y=-
x2+
x+2,
对称轴是:x=1;
(2)直线OA的解析式是y=-x,得点C的坐标是(1,-1).
∵AB=
,BC=
,
∴AB=BC,
又∵OA=
,OC=
,
∴OA=OC,
∴∠ABO=∠CBO.
由直线OB的表达式y=x,得点D的坐标为(1,1).
由直线AB的表达式:y=
x+
,
得直线与x轴的交点E的坐标为(-4,0).
∵△POB与△BCD相似,∠ABO=∠CBO,
∴∠BOP=∠BDC或∠BOP=∠BCD.
①当∠BOP=∠BDC时,由∠BDC=135°,得∠BOP=135°.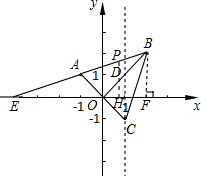
∴点P不但在直线AB上,而且也在x轴上,即点P与点E重合.
∴点P的坐标为(-4,0).
②当∠BOP=∠BCD时,
由△BOP∽△BCD,得:
=
.
而BO=2
,BD=
,BC=
,
∴BP=
,
又∵BE=2
,
∴PE=
,
作PH⊥x轴,垂足是H,BF⊥x轴,垂足是F.
∵PH∥BF,
∴
=
=
,而BF=2,EF=6,
∴PH=
,EH=
.
∴OH=
.
∴点P的坐标是(
,
).
综上所述,点P的坐标为(-4,0)或(
,
).
|
解得:
|
则所求的二次函数的解析式是:y=-
| 1 |
| 3 |
| 2 |
| 3 |
对称轴是:x=1;
(2)直线OA的解析式是y=-x,得点C的坐标是(1,-1).
∵AB=
| 10 |
| 10 |
∴AB=BC,
又∵OA=
| 2 |
| 2 |
∴OA=OC,
∴∠ABO=∠CBO.
由直线OB的表达式y=x,得点D的坐标为(1,1).
由直线AB的表达式:y=
| 1 |
| 3 |
| 4 |
| 3 |
得直线与x轴的交点E的坐标为(-4,0).
∵△POB与△BCD相似,∠ABO=∠CBO,
∴∠BOP=∠BDC或∠BOP=∠BCD.
①当∠BOP=∠BDC时,由∠BDC=135°,得∠BOP=135°.

∴点P不但在直线AB上,而且也在x轴上,即点P与点E重合.
∴点P的坐标为(-4,0).
②当∠BOP=∠BCD时,
由△BOP∽△BCD,得:
| BP |
| BO |
| BD |
| BC |
而BO=2
| 2 |
| 2 |
| 10 |
∴BP=
2
| ||
| 5 |
又∵BE=2
| 10 |
∴PE=
8
| ||
| 5 |
作PH⊥x轴,垂足是H,BF⊥x轴,垂足是F.
∵PH∥BF,
∴
| PH |
| BF |
| PE |
| BE |
| EH |
| EF |
∴PH=
| 8 |
| 5 |
| 24 |
| 5 |
∴OH=
| 4 |
| 5 |
∴点P的坐标是(
| 4 |
| 5 |
| 8 |
| 5 |
综上所述,点P的坐标为(-4,0)或(
| 4 |
| 5 |
| 8 |
| 5 |
点评:此题主要考查了待定系数法求二次函数解析式以及相似三角形的性质和二次函数综合应用,利用数形结合以及分类讨论求出是解题关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为