题目内容
已知实数a,b,c满足 ,则函数y=kx-3的图象必经过第________象限.
,则函数y=kx-3的图象必经过第________象限.
三、四
分析:分类讨论:当a+b+c=0,则a+b=-c,易得k=-1,根据一次函数的性质得到函数y=-x-3的图象经过第二、三、四象限;当a+b+c≠0,根据比例的性质得到k=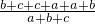 =2,再根据一次函数的性质得函数y=2x-3的图象经过第一、三、四象限;因此判断函数y=kx-3的图象必经过第三象限.
=2,再根据一次函数的性质得函数y=2x-3的图象经过第一、三、四象限;因此判断函数y=kx-3的图象必经过第三象限.
解答:当a+b+c=0,则a+b=-c,
∴k=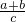 =-1;
=-1;
∴y=-x-3,
∴函数y=-x-3的图象经过第二、三、四象限;
当a+b+c≠0,
∴k=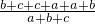 =2,
=2,
∴y=2x-3,
∴函数y=2x-3的图象经过第一、三、四象限;
∴函数y=kx-3的图象必经过第三、四象限.
故答案为三、四.
点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k≠0)的图象为直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;当b>0,图象与y轴的交点在x轴上方;当b=0,图象过原点;当b<0,图象与y轴的交点在x轴下方.也考查了比例的性质.
分析:分类讨论:当a+b+c=0,则a+b=-c,易得k=-1,根据一次函数的性质得到函数y=-x-3的图象经过第二、三、四象限;当a+b+c≠0,根据比例的性质得到k=
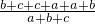 =2,再根据一次函数的性质得函数y=2x-3的图象经过第一、三、四象限;因此判断函数y=kx-3的图象必经过第三象限.
=2,再根据一次函数的性质得函数y=2x-3的图象经过第一、三、四象限;因此判断函数y=kx-3的图象必经过第三象限.解答:当a+b+c=0,则a+b=-c,
∴k=
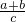 =-1;
=-1;∴y=-x-3,
∴函数y=-x-3的图象经过第二、三、四象限;
当a+b+c≠0,
∴k=
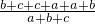 =2,
=2,∴y=2x-3,
∴函数y=2x-3的图象经过第一、三、四象限;
∴函数y=kx-3的图象必经过第三、四象限.
故答案为三、四.
点评:本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k≠0)的图象为直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;当b>0,图象与y轴的交点在x轴上方;当b=0,图象过原点;当b<0,图象与y轴的交点在x轴下方.也考查了比例的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式
(2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式
 (1)已知m是方程x2-x-2=0的一个实数根,求代数式
(1)已知m是方程x2-x-2=0的一个实数根,求代数式 的值.
的值. 的图象交于A、B两点.
的图象交于A、B两点.