��Ŀ����
����Ŀ����ͼ��ij����ɽ���½�![]() �����һ�������ﶥ��
�����һ�������ﶥ��![]() ������Ϊ
������Ϊ![]() ����ɽ�������ߵ�
����ɽ�������ߵ�![]() ���ٲ�øý����ﶥ��
���ٲ�øý����ﶥ��![]() ������Ϊ
������Ϊ![]() ����֪
����֪![]() �ף�
�ף�![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��ɽ���¶�Ϊ
��ɽ���¶�Ϊ![]() ����
����![]() ����ע��ȡ
����ע��ȡ![]() Ϊ
Ϊ![]() ��
��
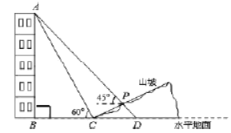
��1����ý�����ĸ߶ȣ���![]() �ij�����
�ij�����
��2�����������λ�õ�![]() ��Ǧֱ�߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
��Ǧֱ�߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
��3����ijһʱ�̣�![]() �׳�ľ������ʱ����̫�������µ�ˮƽӰ����
�׳�ľ������ʱ����̫�������µ�ˮƽӰ����![]() �ף���ͬһʱ�̸��������ﶥ��
�ף���ͬһʱ�̸��������ﶥ��![]() ͶӰ��ɽ���ϵ�
ͶӰ��ɽ���ϵ�![]() �غϣ����
�غϣ����![]() �������������ˮƽ���룮
�������������ˮƽ���룮
���𰸡���1��136����2�������ڵ�λ�õ�P��Ǧֱ�߶�Ϊ14�ף���3��![]()
��������
��1����ACB=60������ABC=90����BC=80���������AB��
��2������P��PE��BD��E��PF��AB��F�����ı���BEPF�Ǿ��Σ�����PE=BF��PF=BE����BF=PE=x����Ϊtan��PCD![]() ��CE=3x����Rt��PAF�У���APF=45����AF=136��x��PF=BE=BC+CE=80+3x������AF=PF���г�����x�ĵ�ʽ���������x��
��CE=3x����Rt��PAF�У���APF=45����AF=136��x��PF=BE=BC+CE=80+3x������AF=PF���г�����x�ĵ�ʽ���������x��
��3�����M��Ǧֱ�߶�Ϊa�ף�![]() ���������a���������
���������a���������![]()
��1���ߡ�ACB=60������ABC=90����BC=80��
��![]()
��![]() ��
��
�ʴ�Ϊ��136
��2������P��PE��BD��E��PF��AB��F��
�֡�AB��BC��
���ı���BEPF�Ǿ��Σ�
��PE=BF��PF=BE��
��PE=x�ף���BF=PE=x�ף�
����Rt��PCE��tan��PCD![]() ��
��
��CE=3x��
����Rt��PAF����APF=45����
��AF=AB��BF=136��x��PF=BE=BC+CE=80+3x��
�֡�AF=PF��
��136��x=80+3x��
��ã�x=14��
�������ڵ�λ�õ�P��Ǧֱ�߶�Ϊ14�ף�

�ʴ�Ϊ��14
��3�����M��Ǧֱ�߶�Ϊa�ף���
![]() �����
�����![]() ��
��
���M�������������ˮƽ����= ![]() �ף�
�ף�
�ʴ�Ϊ��![]()

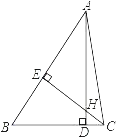
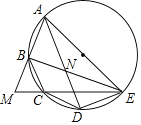
����Ŀ����֤������֪����ͼ��![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ����ʱ����λͬѧ��֤�����£�
����ʱ����λͬѧ��֤�����£�
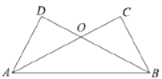
֤��һ���ɹ��ɶ�������
|
֤������
|
��1����˼��������λͬѧ��֤���У���һλͬѧ����ɵ�֤��������һ��������Ѵ������д����
��2������ѡ������һ��֤�������֤����