题目内容
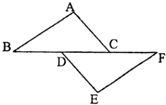
 如图,点E,C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.
如图,点E,C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.(1)求证:AB=DE;
(2)若AC交DE于M,且AB=
 ,ME=
,ME= ,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角∠ECG的度数.
【答案】分析:(1)通过证明△ABC≌△DEF即可得出AB=DE.
(2)要求角的度数就要解直角三角形,根据特殊角的三角函数值来计算.
解答:(1)证明:∵BE=FC,
∴BC=EF,
又∵∠ABC=∠DEF,∠A=∠D,
∴△ABC≌△DEF,(1分)
∴AB=DE.(2分)
 (2)解:∵∠DEF=∠B=45°,
(2)解:∵∠DEF=∠B=45°,
∴DE∥AB,
∴∠CME=∠A=90°,(3分)
∴AC=AB= ,MC=ME=
,MC=ME= ,(4分)
,(4分)
∴在Rt△MEC中,EC= =
= =2,
=2,
∴CG=CE=2,(5分)
在Rt△CAG中,cos∠ACG= =
= ,
,
∴∠ACG=30°,(6分)
∴∠ECG=∠ACB-∠ACG=45°-30°=15°.(7分)
点评:本题综合考查了旋转变换作图,三角形全等和解直角三角形的综合应用.
(2)要求角的度数就要解直角三角形,根据特殊角的三角函数值来计算.
解答:(1)证明:∵BE=FC,
∴BC=EF,
又∵∠ABC=∠DEF,∠A=∠D,
∴△ABC≌△DEF,(1分)
∴AB=DE.(2分)
 (2)解:∵∠DEF=∠B=45°,
(2)解:∵∠DEF=∠B=45°,∴DE∥AB,
∴∠CME=∠A=90°,(3分)
∴AC=AB=
 ,MC=ME=
,MC=ME= ,(4分)
,(4分)∴在Rt△MEC中,EC=
 =
= =2,
=2,∴CG=CE=2,(5分)
在Rt△CAG中,cos∠ACG=
 =
= ,
,∴∠ACG=30°,(6分)
∴∠ECG=∠ACB-∠ACG=45°-30°=15°.(7分)
点评:本题综合考查了旋转变换作图,三角形全等和解直角三角形的综合应用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 18、如图,点D、C在BF上,AB∥EF,∠A=∠E,BC=DF,求证AB=EF.
18、如图,点D、C在BF上,AB∥EF,∠A=∠E,BC=DF,求证AB=EF.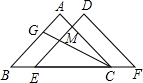 如图,点E,C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°.
如图,点E,C在BF上,BE=FC,∠ABC=∠DEF=45°,∠A=∠D=90°. 17、如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
17、如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,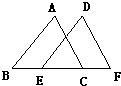 14、如图,点E,C在BF上,AB=DE,∠ABC=∠DEF,请你补充一个条件
14、如图,点E,C在BF上,AB=DE,∠ABC=∠DEF,请你补充一个条件 (2012•浦江县模拟)如图,点D、C在BF上,AB∥EF,BD=CF,请添上一个条件,使AC=DE成立,并证明.
(2012•浦江县模拟)如图,点D、C在BF上,AB∥EF,BD=CF,请添上一个条件,使AC=DE成立,并证明.