题目内容
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF. 
(1)求证:△BOE≌△DOF;
(2)若OA= ![]() BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵BE⊥AC,DF⊥AC
∴∠BEO=90°=∠DFO,
在△BOE和△DOF中,

∴△BOE≌△DOF(ASA)
(2)解:四边形ABCD是矩形
证明:∵△BOE≌△DOF,
∴OB=OD,
∵OE=OF,CE=AF,
∴OC=OA,
∴四边形ABCD是平行四边形,
∴OA= ![]() AC,
AC,
又∵OA= ![]() BD,
BD,
∴AC=BD
∴□ABCD是矩形
【解析】(1)根据AAS或ASA即可证明;(2)结论:矩形.只要证明对角线AC=BD即可;

练习册系列答案
相关题目
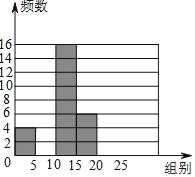
【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.