题目内容
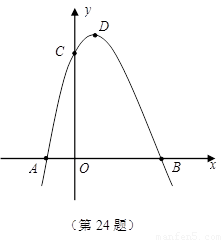
如图,抛物线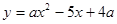 与
与 轴相交于点
轴相交于点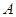 、
、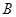 ,且经过点
,且经过点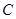 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为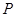 .
.
(1)求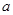 的值和该抛物线顶点
的值和该抛物线顶点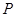 的坐标.
的坐标.
(2)求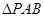 的面积;
的面积;
(3)若将该抛物线先向左平移4个单位,再向上平移2个单位,求出平移后抛物线的解析式.
(1)点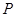 的坐标为(
的坐标为(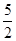 ,
,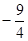 ) (2)
) (2)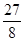 (3)
(3)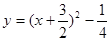
解析试题分析:(1)根据C点的坐标代入抛物线解析式y=ax2-5x+4a,求出a,即可得出抛物线解析式,再根据抛物线顶点坐标公式即可求出答案;
(2)根据y=x2-5x+4中y=0时,求出x的值,从而得出A、B两点的坐标,再根据三角形的面积公式得出△PAB的面积;
(3)根据抛物线原顶点坐标和平移后的顶点,即可得出平移后抛物线解析式;
解:(1)将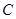 (5,4)的坐标代入抛物线解析式
(5,4)的坐标代入抛物线解析式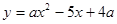 , 得
, 得 ;
;
∴抛物线解析式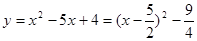
∴点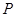 的坐标为(
的坐标为(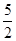 ,
,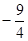 );
);
(2)∵当 中
中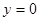 时,
时,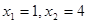 ,
,
∴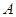 、
、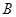 两点的坐标为
两点的坐标为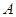 (1,0),
(1,0),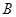 (4,0),
(4,0),
∴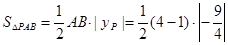 =
=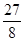
(3)∵抛物线原顶点坐标为(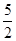 ,
,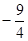 ),
),
平移后的顶点为(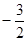 ,
, )
)
∴平移后抛物线解析式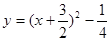
考点:用待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变化,三角形面积.
点评:此题考查了待定系数法求二次函数的解析式;关键是能根据二次函数的性质,三角形的面积,二次函数的图象与几何变换分别进行求解.

练习册系列答案
相关题目
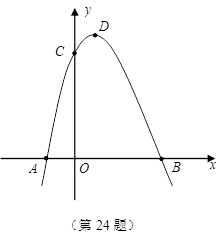
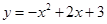 与
与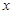 轴相交于
轴相交于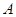 、
、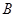 两点(点
两点(点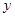 轴相交于点
轴相交于点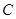 ,顶点为
,顶点为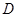 .
.
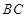 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点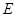 ,点
,点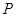 为线段
为线段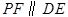 交抛物线于点
交抛物线于点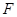 ,设点
,设点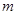 ;
;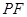 的长,并求出当
的长,并求出当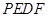 为平行四边形?
为平行四边形?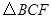 的面积为
的面积为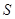 ,求
,求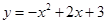 与
与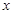 轴相交于
轴相交于 、
、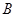 两点(点
两点(点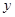 轴相交于点
轴相交于点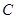 ,顶点为
,顶点为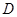 .
.
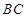 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点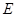 ,点
,点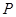 为线段
为线段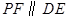 交抛物线于点
交抛物线于点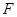 ,设点
,设点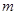 ;
;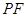 的长,并求出当
的长,并求出当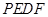 为平行四边形?
为平行四边形?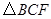 的面积为
的面积为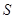 ,求
,求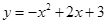 与
与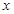 轴相交于
轴相交于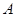 、
、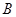 两点(点
两点(点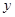 轴相交于点
轴相交于点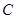 ,顶点为
,顶点为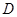 .
.
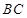 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点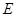 ,点
,点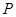 为线段
为线段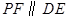 交抛物线于点
交抛物线于点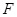 ,设点
,设点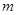 ;
;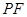 的长,并求出当
的长,并求出当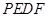 为平行四边形?
为平行四边形?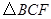 的面积为
的面积为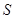 ,求
,求