题目内容
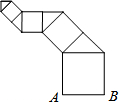 (2013•营口)按如图方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2,…,则第n个正方形与第n个等腰直角三角形的面积和Sn=
(2013•营口)按如图方式作正方形和等腰直角三角形.若第一个正方形的边长AB=1,第一个正方形与第一个等腰直角三角形的面积和为S1,第二个正方形与第二个等腰直角三角形的面积和为S2,…,则第n个正方形与第n个等腰直角三角形的面积和Sn=| 5 |
| 2n+1 |
| 5 |
| 2n+1 |
分析:观察图形,根据正方形的四条边相等和等腰直角三角形的腰长为斜边长的
倍,分别求得每个正方形的边长,从而发现规律,再根据规律解题即可.
| ||
| 2 |
解答:解:∵第一个正方形的边长为1,
第2个正方形的边长为(
)1=
,
第3个正方形的边长为(
)2=
,
…,
第n个正方形的边长为(
)n-1,
∴第n个正方形的面积为:[(
)2]n-1=
,
则第n个等腰直角三角形的面积为:
×
=
,
故第n个正方形与第n个等腰直角三角形的面积和Sn=
+
=
.
故答案为:
.
第2个正方形的边长为(
| ||
| 2 |
| ||
| 2 |
第3个正方形的边长为(
| ||
| 2 |
| 1 |
| 2 |
…,
第n个正方形的边长为(
| ||
| 2 |
∴第n个正方形的面积为:[(
| ||
| 2 |
| 1 |
| 2n-1 |
则第n个等腰直角三角形的面积为:
| 1 |
| 2n-1 |
| 1 |
| 4 |
| 1 |
| 2n+1 |
故第n个正方形与第n个等腰直角三角形的面积和Sn=
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 5 |
| 2n+1 |
故答案为:
| 5 |
| 2n+1 |
点评:此题主要考查了正方形的性质以及等腰直角三角形的性质和直角边长是斜边长的
倍及正方形的面积公式求解.找到第n个正方形的边长为(
)n-1是解题的关键.
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
