题目内容
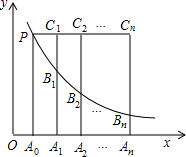 如图,直线y=k和双曲线y=
如图,直线y=k和双曲线y=| k |
| x |
| k |
| x |
| CnBn |
| AnBn |
分析:求A0点坐标关键求其横坐标,而它的横坐标就是点P横坐标,解方程组
即得,然后求出
及
的值,方法是求出各自线段长度即求出各点纵坐标即解,依此类推得到
的值,从而归纳总结得到
的值.
|
| C1B1 |
| A1B1 |
| C2B2 |
| A2B2 |
| C3B3 |
| A3B3 |
| CnBn |
| AnBn |
解答:解:依题意得点A0坐标满足
,
∴x=1,
∴点A0坐标为(1,0);
由于A0、A1、A2点的横坐标为连续整数,
∴A1、A2点的坐标为(2,0)、(3,0).
∴A1B1=
,A2B2=
,
∴
=
=1,
=
=2;
同理
=
=3,
则
=n.
故答案为:n
|
∴x=1,
∴点A0坐标为(1,0);
由于A0、A1、A2点的横坐标为连续整数,
∴A1、A2点的坐标为(2,0)、(3,0).
∴A1B1=
| k |
| 2 |
| k |
| 3 |
∴
| C1B1 |
| A1B1 |
k-
| ||
|
| C2B2 |
| A2B2 |
k-
| ||
|
同理
| C3B3 |
| A3B3 |
k-
| ||
|
则
| CnBn |
| AnBn |
故答案为:n
点评:此题难度中等,主要考查反比例函数的图象和性质,通过图象找到题目要求的规律是解决此题的关键,同学们要熟练掌握.

练习册系列答案
相关题目
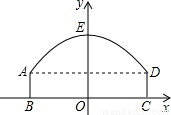
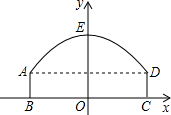 线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=