题目内容
如图,直线AB与CD相交于点0,射线OE平分∠BOF,∠AOD+∠COB=40°,∠DOF:∠FOB=1 :7.
:7.(1)求∠AOD和∠EOB的度数;
(2)你发现射线OD是一条什么特殊的线?请说明理由;
(3)你发现射线OE与直线CD有什么位置关系?请说明理由.
分析:(1)根据∠AOD和∠COB是对顶角容易求出∠AOD=∠BOC=20°,所以∠DOB等于160°,再根据两角之比为1:7求出∠BOF等于140°,所以∠EOB等于70°;
(2)根据角的度数之比可以求出∠DOF等于20°,所以OD为∠AOF的角平分线;
(3)根据所求角的度数可以求出∠EOC等于90°,所以OE⊥CD.
(2)根据角的度数之比可以求出∠DOF等于20°,所以OD为∠AOF的角平分线;
(3)根据所求角的度数可以求出∠EOC等于90°,所以OE⊥CD.
解答:解:(1)∵∠AOD+∠COB=40°,∠AOD=∠COB,
∴∠AOD=20°,
∴∠DOB=180°-20°=160°,
∵∠DOF:∠FOB=l:7,
∴∠BOF=
×160°=140°,
∵OE平分∠BOF,
∴∠BOE=
∠BOF=
×140°=70°;
(2)∠DOF=
×160°=20°,
∴∠AOD=∠DOF,
∴OD是∠AOF的平分线;
(3)∵∠EOC=∠BOE+∠COB=70°+20°=90°,
∴OE⊥CD.
∴∠AOD=20°,
∴∠DOB=180°-20°=160°,
∵∠DOF:∠FOB=l:7,
∴∠BOF=
| 7 |
| 1+7 |
∵OE平分∠BOF,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∠DOF=
| 1 |
| 1+7 |
∴∠AOD=∠DOF,
∴OD是∠AOF的平分线;
(3)∵∠EOC=∠BOE+∠COB=70°+20°=90°,
∴OE⊥CD.
点评:本题主要利用对顶角相等,垂线的定义和角平分线的定义求解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
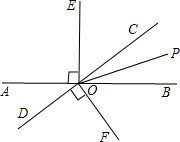 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.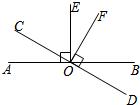 8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对:
8、如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.则图中除了直角相等外,还有相等的角,请写出三对: 10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有
10、如图,直线AB与CD相交于O点,且∠COE=90°,则与∠EOA互余的角有 如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=
如图,直线AB与CD相交于点O,∠AOC=65°,则∠DOB=