题目内容
如图,点C是线段AB上任意一点,分别以AC、BC为边在同侧作等边△ACD和等边△BCE,连接BD、AE.
(1)试找出图中能够通过旋转完全重合的图形,并说明它是绕哪一点旋转?旋转了多少度?
(2)说出AE与DB有什么关系,试用旋转的性质说明上述关系成立的理由.

解:(1)∵△ACD和△BCE都为等边三角形,
∴CA=CD,CE=CB,∠ACD=∠BCE=60°,
∴将△ACE绕点C顺时针旋转60°可得到△DCB,旋转角等于60°.
(2)AE=DB.理由如下:
∵△ACE绕点C顺时针旋转60°得到△DCB,
根据旋转前后的两个图形全等,
∴AE=BD.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
如图,点C是线段AB的中点,点D是线段BC的中点,下面等式不正确的是( )
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
 10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )
10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )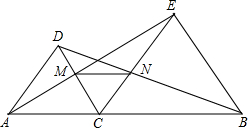 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( ) 如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )