题目内容
 在△ABC中,∠ACB=90°,M是AB的中点,E、F分别是AC、BC延长线上的点,且CE=CF=
在△ABC中,∠ACB=90°,M是AB的中点,E、F分别是AC、BC延长线上的点,且CE=CF= AB,则∠EMF的度数为________.
AB,则∠EMF的度数为________.
45°
分析:首先连接CM,根据直角三角形斜边上的中线等于斜边的一半可得到CM= AB,再结合条件CE=CF=
AB,再结合条件CE=CF= AB,可得CE=MC,CF=MC,从而得到∠1=∠E,∠2=∠F,再利用三角形内角与外角的关系可得∠1+∠E=∠4,∠2+∠F=∠3,进而得到∠1=
AB,可得CE=MC,CF=MC,从而得到∠1=∠E,∠2=∠F,再利用三角形内角与外角的关系可得∠1+∠E=∠4,∠2+∠F=∠3,进而得到∠1= ∠4,∠2=
∠4,∠2= ∠3,再结合∠3+∠4=90°可算出∠EMF的度数.
∠3,再结合∠3+∠4=90°可算出∠EMF的度数.
解答: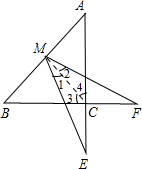 解:连接CM,
解:连接CM,
∵∠ACB=90°,M是AB的中点,
∴CM= AB,AM=BM=
AB,AM=BM= AB,
AB,
∵CE=CF= AB,
AB,
∴CE=MC,CF=MC,
∴∠1=∠E,∠2=∠F,
∵∠1+∠E=∠4,∠2+∠F=∠3,
∴∠1= ∠4,∠2=
∠4,∠2= ∠3,
∠3,
∴∠1+∠2= (∠4+∠3)=
(∠4+∠3)= ×90°=45°,
×90°=45°,
即:∠EMF=45°.
故答案为:45°.
点评:此题主要考查了直角三角形的性质,以及三角形内角与外角的关系,关键是根据条件得到∠1= ∠4,∠2=
∠4,∠2= ∠3.
∠3.
分析:首先连接CM,根据直角三角形斜边上的中线等于斜边的一半可得到CM=
 AB,再结合条件CE=CF=
AB,再结合条件CE=CF= AB,可得CE=MC,CF=MC,从而得到∠1=∠E,∠2=∠F,再利用三角形内角与外角的关系可得∠1+∠E=∠4,∠2+∠F=∠3,进而得到∠1=
AB,可得CE=MC,CF=MC,从而得到∠1=∠E,∠2=∠F,再利用三角形内角与外角的关系可得∠1+∠E=∠4,∠2+∠F=∠3,进而得到∠1= ∠4,∠2=
∠4,∠2= ∠3,再结合∠3+∠4=90°可算出∠EMF的度数.
∠3,再结合∠3+∠4=90°可算出∠EMF的度数.解答:
 解:连接CM,
解:连接CM,∵∠ACB=90°,M是AB的中点,
∴CM=
 AB,AM=BM=
AB,AM=BM= AB,
AB,∵CE=CF=
 AB,
AB,∴CE=MC,CF=MC,
∴∠1=∠E,∠2=∠F,
∵∠1+∠E=∠4,∠2+∠F=∠3,
∴∠1=
 ∠4,∠2=
∠4,∠2= ∠3,
∠3,∴∠1+∠2=
 (∠4+∠3)=
(∠4+∠3)= ×90°=45°,
×90°=45°,即:∠EMF=45°.
故答案为:45°.
点评:此题主要考查了直角三角形的性质,以及三角形内角与外角的关系,关键是根据条件得到∠1=
 ∠4,∠2=
∠4,∠2= ∠3.
∠3. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
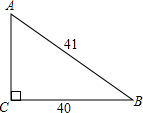 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=