题目内容
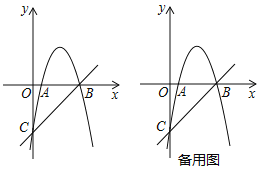
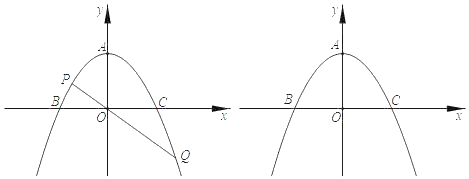
【题目】已知:如图,抛物线![]() 的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=2OP.若点Q正好落在该抛物线上,求点P的坐标;
(3)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=mOP(m为常数);
①证明点Q一定落在抛物线![]() 上;
上;
②设有一个边长为m+1的正方形(其中m>3),它的一组对边垂直于x轴,另一组对边垂直于y轴,并且该正方形四个顶点正好落在抛物线![]() 和
和![]() 组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
【答案】(1)![]() (2)(
(2)(![]() ,1)(-
,1)(-![]() ,1)(3)①见解析②当点Q与正方形右下或左下顶点重合时,PQ被正方形上下两边所截线段最长,此时点Q的坐标为(2+
,1)(3)①见解析②当点Q与正方形右下或左下顶点重合时,PQ被正方形上下两边所截线段最长,此时点Q的坐标为(2+![]() ,-5-4
,-5-4![]() )或(-2-
)或(-2-![]() ,-5-4
,-5-4![]() ).
).
【解析】
(1)用两点式求出抛物线解析式;
(2)设点P坐标,作PE⊥x轴,FQ⊥x轴,利用相似关系求出点Q坐标,因为点Q在抛物线上,所以将点Q坐标代入解析式,求得点P坐标;
(3)①同(2)的方法,求出点Q坐标代入y2解析式,可证明点Q在抛物线y2上;
②因为y1与y2抛物线都是以y轴为对称轴的抛物线,所以正方形也是以y轴对称,从而获得正方形右侧点的横坐标,代入各自解析式获得纵坐标,以右侧两点的纵坐标做差等于正方形边长,列出方程求出m的值,从而获得正方形四个顶点的坐标,由图可知,当Q点与正方形的左下和右下端点重合时PQ被正方形所截的线段最大,从而获得点Q坐标.
解:(1)由条件可设抛物线y1=ax2+2,将C(2,0)代入
可得抛物线![]() ;
;
(2)如图,作PE⊥x轴,FQ⊥x轴
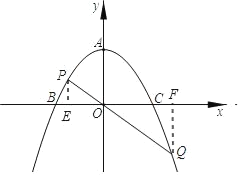
设点P(t,![]() ),
),
利用△PEO∽△OFQ可求得点Q(﹣2t,t2﹣4).
把Q(﹣2t,t2﹣4)代入![]() 中,
中,
得:t2﹣4=![]() ,
,
∴3t2=6,
∴t=±![]() ,
,
∴P1(![]() ,1),P2(
,1),P2(![]() ,1);
,1);
(3)①证明:设点P(t,![]() ),
),
利用相似可求得点Q(﹣mt,![]() ).
).
将x=﹣mt代入![]() 中,
中,
得:![]()
![]() .
.
∴点Q一定落在抛物线![]() 上;
上;
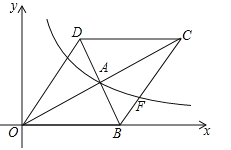
②如图所示
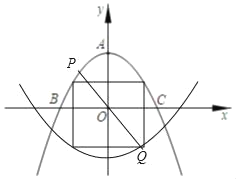
∵正方形的边长为m+1,
由抛物线的对称性可知
正方形右边两个顶点横坐标为![]() ,
,
将x=![]() 代入抛物线解析式
代入抛物线解析式
可得两点纵坐标分别为:![]() 和
和![]() ,
,
∴![]() -
-![]() =m+1,
=m+1,
解得:![]() .
.
∵m>3,
∴![]() .
.
∴正方形右边两个顶点横坐标为![]() ,
,
将x=![]() 代入
代入![]() 得:
得:
![]() ,
,
∴正方形右下顶点的纵坐标为![]() .
.
∴正方形右下顶点的坐标为(![]() ),
),
同理,正方形左下顶点的坐标为(![]() ,
,![]() ).
).
设PQ与y轴所成的角为α,当PQ与正方形上下两边相交时,
PQ被正方形上下两边所截线段的长![]() ,
,
当α增大时,cosα减小,![]() 增大,
增大,
当PQ经过正方形右下顶点时,α最大,PQ被正方形上下两边所截线段最大,此时点Q与正方形右下或左下顶点重合;
当PQ与正方形上右两边(或上左两边)相交时,由图形可知随着α的增大,PQ被正方形上下两边所截线段的长减小,
综上所述,当点Q与正方形右下或左下顶点重合时,PQ被正方形上下两边所截线段最长,
此时点Q的坐标为(![]() )或(
)或(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 9~10分 | x | m |
B | 8~7 | 23 | 0.46 |
C | 6~5 | y | n |
D | 5分以下 | 3 | 0.06 |
(1)试直接写出x,y,m,n的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?