Question

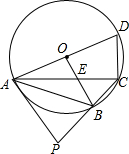（2012•香洲区一模）如图，四边形ABCD内接于⊙O，已知直径AD=4，∠ABC=120°，∠ACB=45°，连接OB交AC于点E．
（1）求AC的长；
（2）求CE：AE的值；
（3）在CB的延长线上取一点P，使PB=2BC，试判断直线PA和⊙O的位置关系，并证明你的结论．

Answer 1

分析：（1）过点O作OF⊥AC于点F．由三角形内角和定理求得△ACB的内角∠CAB=15°，根据圆周角定理知∠COB=2∠CAB=30°、∠AOB=2∠ACB=90°；然后在直角△AOF中利用余弦三角函数的定义即可求得AC的长度；
（2）连接OC，由∠ABC和∠ACB的度数求出∠AOB，∠OAC，∠OCA和∠COE的度数，利用直角三角形以及等腰三角形得到AE与EC的关系；
（3）直线PA和⊙O相切于点A．根据对应线段的比相等判定AP与OB平行，再用两直线平行，同旁内角互补，得到∠OAP=90°，判定PA切⊙O于点A．

解答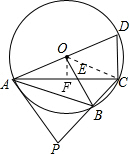：解：（1）过点O作OF⊥AC于点F．则AF=CF（垂径定理）；
∵∠ACB=45°，∠AOB=2∠ACB，（同弧所对的圆周角是所对的圆心角的一半），
∴∠AOB=90°；
又∵在△ABC中，∠ABC=120°，∠ACB=45°，
∴∠CAB=15°（三角形内角和定理），
∴∠COB=2∠CAB=30°（同弧所对的圆周角是所对的圆心角的一半），
∴∠AOC=120°；
∵OA=OC=2（⊙O的半径），
∴∠OAC=∠OCA=30°（等边对等角），
∴AF=OA•cos∠OAF=2×

3

2

=

3

，
∴AC=2AF=2

3

；

（2）如图：连接OC．由（1）知，∠AOB=90°，∠E0C=∠ECO=∠OAE=30°．
则在直角△AOE中，设OE=a，则AE=2a，CE=a，
∴

CE

AE

=

a

2a

=

1

2

；

（3）直线PA和⊙O相切于点A．理由如下：
由（2）知，

CE

AE

=

1

2

．
∵PB=2BC，
∴

BC

PB

=

1

2

．
∴

EC

AE

=

BC

PB

=

1

2

，
∵∠ACB=∠ACB，
∴△CEB∽△CAP，
∴∠CBE=∠P，
∴OB∥AP，
∴∠OAP+∠AOB=180°，
∴∠OAP=90°，
∵O为半径，
∴PA切⊙O于点A．

点评：本题考查的是圆的综合题：在同圆或等圆中，同弧所对的圆周角是所对的圆心角的一半，；垂直于弦的直径平分弦；运用余弦的定义进行几何计算；根据题目的条件求出相应的角的度数，利用线段的比相等判定两直线平行，用两直线平行同旁内角互补得到∠OAP=90°，证明AD切⊙O于点A．