题目内容
如图,在![]() 中,
中,![]() ,
,![]() =3,
=3,![]() =4,⊙
=4,⊙![]() 是
是![]() 的内切圆,点
的内切圆,点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]() .
.

2
解析:连接OE、OF、OQ,设⊙O的半径是r,
由勾股定理得:AB= ![]() =5,
=5,
∵⊙O是三角形ABC的内切圆,
∴OE⊥AC,OF⊥BC,OE=OF,AE=AQ,BF=BQ,
∵∠C=90°,
∴∠C=∠CFO=∠CEO=90°,
∴四边形CFOE是正方形,
∴CE=CF=OF=OE,
∴3-r+4-r=5,
r=1,AQ=AE=3-1=2,OQ=1,
∵D是AB的中点,
∴AD= ![]() ,
,
∴DQ=AD-AQ= ![]() ,
,
tan∠ODA=  =2
=2

练习册系列答案
相关题目
 中,
中, 是
是 边上的高,
边上的高, 是
是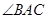 平分线。求
平分线。求 的度数。
的度数。
 中,
中, ,
, 平分
平分 交
交 于
于 ,点
,点 在
在 上,以
上,以 为半径的圆,交
为半径的圆,交 ,交
,交 于
于 ,且点
,且点 ,切⊙
,切⊙


 ,求⊙
,求⊙ 中,
中, D是BC上的点,
D是BC上的点,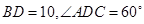 .求AC(
.求AC(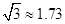 ,结果保留整数).
,结果保留整数).
 中,
中, ,点
,点 在
在 上,以
上,以 长为半径的圆与
长为半径的圆与 分别交于点
分别交于点 ,且
,且 .
. 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; ,
, ,求
,求 的值.
的值.