题目内容
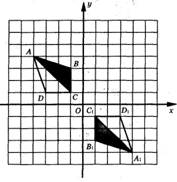
如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.(1)写出点D1的坐标______,点D旋转到点D1所经过的路线长______

【答案】分析:(1)写出D点的坐标后,相当于将四边形以原点为位似中心作位似比为1的位似变换;点D所经过的线路实际上是一个半圆的弧长;
(2)根据图中所给角从中找到特殊的角,写出这个特殊角的三角函数值即可;
(3)根据某点的坐标的变化来得到这个图象的平移规律,根据此平移规律描出其他各点,顺次连接即可画出平移后的图形.
解答: 解:(1)如图:点D的坐标为(-3,1),
解:(1)如图:点D的坐标为(-3,1),
∵将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1,
∴点D1的坐标为:(3,-l),
由勾股定理得:OD= =
= ,
,
∴点D旋转到点D1所经过的路线长= =
= π;
π;
(2)∠ACD, (或∠DAC,
(或∠DAC, );
);
(3)正确图形如图所示:
点评:本题考查了弧长的计算、锐角三角函数的定义及平移变换等知识,是一道综合性很强的题目,解题时要分清平移和旋转的区别.
(2)根据图中所给角从中找到特殊的角,写出这个特殊角的三角函数值即可;
(3)根据某点的坐标的变化来得到这个图象的平移规律,根据此平移规律描出其他各点,顺次连接即可画出平移后的图形.
解答:
 解:(1)如图:点D的坐标为(-3,1),
解:(1)如图:点D的坐标为(-3,1),∵将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1,
∴点D1的坐标为:(3,-l),
由勾股定理得:OD=
 =
= ,
,∴点D旋转到点D1所经过的路线长=
 =
= π;
π;(2)∠ACD,
 (或∠DAC,
(或∠DAC, );
);(3)正确图形如图所示:
点评:本题考查了弧长的计算、锐角三角函数的定义及平移变换等知识,是一道综合性很强的题目,解题时要分清平移和旋转的区别.

练习册系列答案
相关题目
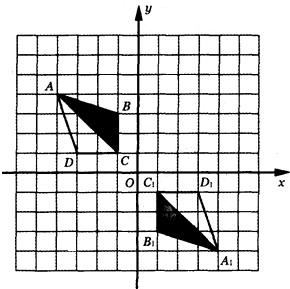 如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.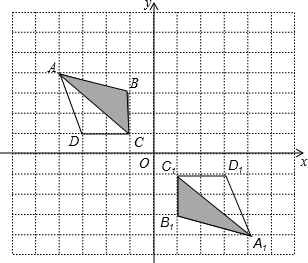 ,5),画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
,5),画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)