题目内容
如图,在平面直角坐标系中,点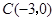 ,点
,点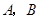 分别在
分别在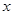 轴,
轴,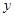 轴的正半轴上,且满足
轴的正半轴上,且满足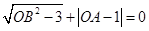 .
.
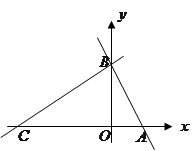
小题1:求点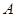 ,点
,点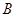 的坐标
的坐标
小题2:若点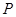 从
从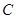 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段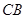 运动,连结
运动,连结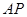 .设
.设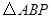 的面积为
的面积为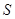 ,点
,点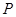 的运动时间为
的运动时间为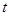 秒,求
秒,求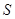 与
与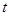 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
小题3:在(2)的条件下,是否存在点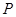 ,使以点
,使以点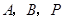 为顶点的三角形与
为顶点的三角形与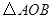 相似?若存在,请直接写出点
相似?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
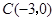 ,点
,点 分别在
分别在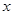 轴,
轴,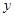 轴的正半轴上,且满足
轴的正半轴上,且满足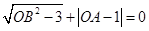 .
.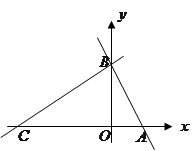
小题1:求点
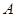 ,点
,点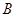 的坐标
的坐标小题2:若点
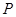 从
从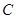 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段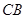 运动,连结
运动,连结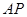 .设
.设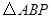 的面积为
的面积为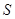 ,点
,点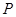 的运动时间为
的运动时间为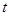 秒,求
秒,求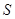 与
与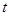 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.小题3:在(2)的条件下,是否存在点
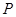 ,使以点
,使以点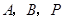 为顶点的三角形与
为顶点的三角形与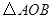 相似?若存在,请直接写出点
相似?若存在,请直接写出点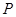 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.小题1:

小题2:

小题3:

本题是一道综合性较强的题目,根据非负数的意义确定OA、OB的长度,从而得出A、B两点的坐标.利用勾股定理得出线段BC、AB长度,利用勾股定理逆定理判定出三角形ABC是直角三角形.将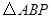 的面积转为三角形ABC的面积与三角形APC的面积的差.
的面积转为三角形ABC的面积与三角形APC的面积的差.
利用相似三角形的性质确定三角形APC底边AC上的高PQ.两个三角形相似时,没有给出具体的对应点,所以需要分类讨论:①当△ABP∽△AOB时,得P(-3,0),②当△ABP∽△BOA时,得P(-1, )
)
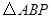 的面积转为三角形ABC的面积与三角形APC的面积的差.
的面积转为三角形ABC的面积与三角形APC的面积的差.利用相似三角形的性质确定三角形APC底边AC上的高PQ.两个三角形相似时,没有给出具体的对应点,所以需要分类讨论:①当△ABP∽△AOB时,得P(-3,0),②当△ABP∽△BOA时,得P(-1,
 )
)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,量得树干倾斜角
,量得树干倾斜角 ,大树被折断部分和坡面所成的角
,大树被折断部分和坡面所成的角 .
.
 的度数;
的度数; ,
, ,
, ).
).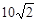 海里.求:
海里.求:

 交AC于点E,F是
交AC于点E,F是
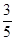 ,AE=
,AE=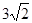 ,求sinF的值和AF的长.
,求sinF的值和AF的长.


 。
。 的值。
的值。