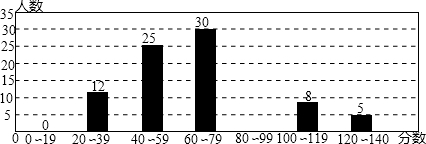
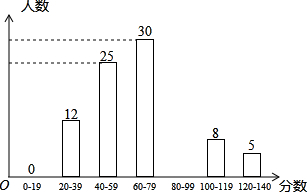
题目内容
已知m、n是整数,3m+2=5n+3,且3m+2>30,5n+3<40,则mn的值是
- A.70
- B.72
- C.77
- D.84
D
分析:根据条件即可得到一个关于m的不等式组和一个关于n的不等式组,即可求得m,n的范围,再根据m,n是整数,以及3m+2=5n+3即可确定m,n的值,进而求解.
解答:解 ,
,
得:m> ,m<
,m< ,
,
即 <m<
<m< ,
,
因为m是整数,因而m=10或11或12.
 ,
,
解得: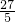 <n<
<n<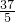 ,
,
因n是整数,则n=6或7.
根据3m+2=5n+3成立时,m=12,n=7,
则mn=12×7=84.
故选D.
点评:本题考查了一元一次不等式的求解,正确求得m,n的值是解决本题的关键.
分析:根据条件即可得到一个关于m的不等式组和一个关于n的不等式组,即可求得m,n的范围,再根据m,n是整数,以及3m+2=5n+3即可确定m,n的值,进而求解.
解答:解
 ,
,得:m>
 ,m<
,m< ,
,即
 <m<
<m< ,
,因为m是整数,因而m=10或11或12.
 ,
,解得:
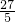 <n<
<n<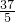 ,
,因n是整数,则n=6或7.
根据3m+2=5n+3成立时,m=12,n=7,
则mn=12×7=84.
故选D.
点评:本题考查了一元一次不等式的求解,正确求得m,n的值是解决本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目