题目内容
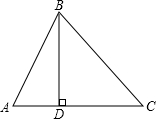 在△ABC中,BD⊥AC,垂足为D点,已知,AB=8,AD=4,∠ABC=75°.
在△ABC中,BD⊥AC,垂足为D点,已知,AB=8,AD=4,∠ABC=75°.
求:∠A,BC.
解:∵BD⊥AC,AB=8,AD=4,
∴∠ABD=30°,
∴∠A=90°-∠ABD=60°;
在Rt△ABD中,BD=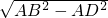 =4
=4 ,
,
∵∠ABC=75°,∠ABD=30°,
∴∠DBC=45°,
∴△BDC是等腰直角三角形,
∴BC= BD=4
BD=4 .
.
综上可得∠A=60°,BC=4 .
.
分析:根据AD=4,AB=8,可得出∠ABD=30°,继而得出∠A;由∠ABC=75°,∠ABD=30°可得出∠DBC=45°,继而得出BC= BD.
BD.
点评:本题考查了勾股定理、等腰直角三角形及含30°角的直角三角形的性质,属于基础题,解答本题的关键是确定出∠ABD=30°,难度一般.
∴∠ABD=30°,
∴∠A=90°-∠ABD=60°;
在Rt△ABD中,BD=
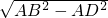 =4
=4 ,
,∵∠ABC=75°,∠ABD=30°,
∴∠DBC=45°,
∴△BDC是等腰直角三角形,
∴BC=
 BD=4
BD=4 .
.综上可得∠A=60°,BC=4
 .
.分析:根据AD=4,AB=8,可得出∠ABD=30°,继而得出∠A;由∠ABC=75°,∠ABD=30°可得出∠DBC=45°,继而得出BC=
 BD.
BD.点评:本题考查了勾股定理、等腰直角三角形及含30°角的直角三角形的性质,属于基础题,解答本题的关键是确定出∠ABD=30°,难度一般.

练习册系列答案
相关题目
 18、已知,如图,在△ABC中,BD⊥AC于D,若∠A:∠ABC:∠ACB=3:4:5,试求∠ABD的度数.
18、已知,如图,在△ABC中,BD⊥AC于D,若∠A:∠ABC:∠ACB=3:4:5,试求∠ABD的度数. 23、如图,在△ABC中,BD是∠ABC的平分线,DF⊥AB于F,DE⊥BC于E.求证BD⊥EF.
23、如图,在△ABC中,BD是∠ABC的平分线,DF⊥AB于F,DE⊥BC于E.求证BD⊥EF. 如图,在△ABC中,BD,CD分别是∠ABC、∠ACB的平分线,BP、CP分别是∠EBC、∠FCB的平分线,且它们分别交于D、P.
如图,在△ABC中,BD,CD分别是∠ABC、∠ACB的平分线,BP、CP分别是∠EBC、∠FCB的平分线,且它们分别交于D、P. 如图在△ABC中,BD平分∠ABC且BD⊥AC于D,DE∥BC与AB相交于E.AB=5cm、AC=2cm,则△ADE的周长=( )
如图在△ABC中,BD平分∠ABC且BD⊥AC于D,DE∥BC与AB相交于E.AB=5cm、AC=2cm,则△ADE的周长=( )