题目内容
如图,OA、OB的长分别是关于x的方程 的两根,且
的两根,且 。请解答下列问题:
。请解答下列问题:

(1)求直线AB的解析式;
(2)若P为AB上一点,且 ,求过点P的反比例函数的解析式。
,求过点P的反比例函数的解析式。
【答案】
(1)直线AB的解析式为 ;(2)
;(2)
【解析】
试题分析:(1)首先解方程 ,即可求得点A与B的坐标,然后利用待定系数法即可求得直线AB的解析式;
,即可求得点A与B的坐标,然后利用待定系数法即可求得直线AB的解析式;
(2)首先过点P作PH⊥x轴于点H,由 ,利用平行线分线段成比例定理,即可求得AH的长,则可求得点P的横坐标,代入一次函数解析式,即可求得点P的坐标,再利用待定系数法即可求得过点P的反比例函数的解析式.
,利用平行线分线段成比例定理,即可求得AH的长,则可求得点P的横坐标,代入一次函数解析式,即可求得点P的坐标,再利用待定系数法即可求得过点P的反比例函数的解析式.
(1)∵
∴ ,解得
,解得 ,
,
∵OA、OB的长分别是关于x的方程 的两根,且
的两根,且 ,
,
∴OA=8,OB=4.
∴A(-8,0),B(0,4).
设直线AB的解析式为y=kx+b,则
 ,解得
,解得
则直线AB的解析式是 ;
;
(2)过点P作PH⊥x轴于点H

设P(x,y),
∴AH=|-8-x|=x+8.
∵PH∥y轴,

解得 x=-6.
∵点P在 上,
上,
∴y= ×(-6)+4=1.
×(-6)+4=1.
∴P(-6,1).
设过点P的反比例函数的解析式为
则 ,解得
,解得
所以过点P的反比例函数的解析式为 .
.
考点:解一元二次方程,待定系数求函数解析式,平行线分线段成比例定理
点评:待定系数求函数解析式是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
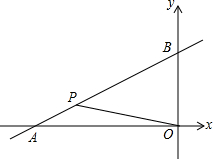 如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题:
如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题: (2012•牡丹江)如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题:
(2012•牡丹江)如图,OA、OB的长分别是关于x的方程x2-12x+32=0的两根,且OA>OB.请解答下列问题:

 ,求过点P的反比例函数的解析式;
,求过点P的反比例函数的解析式;