Question

【题目】如图，在平面直角坐标系中，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．

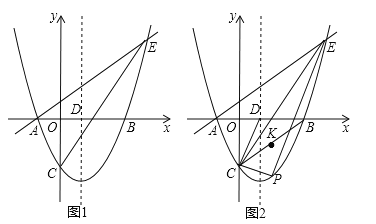
（1）求直线AE的解析式；

（2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值；

（3）点G是线段CE的中点，将抛物线沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在一点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）3；（3）Q的坐标为（3，）或′（3，）或（3，）或（3，）．

【解析】

试题分析：（1）抛物线的解析式可变形为y=（x+1）（x﹣3），从而可得到点A和点B的坐标，然后再求得点E的坐标，设直线AE的解析式为y=kx+b，将点A和点E的坐标代入求得k和b的值，从而得到AE的解析式；

（2）设直线CE的解析式为y=mx﹣，将点E的坐标代入求得m的值，从而得到直线CE的解析式，过点P作PF∥y轴，交CE与点F．设点P的坐标为（x，），则点F（x，），则FP=．由三角形的面积公式得到△EPC的面积=，利用二次函数的性质可求得x的值，从而得到点P的坐标，作点K关于CD和CP的对称点G、H，连接G、H交CD和CP与N、M．然后利用轴对称的性质可得到点G和点H的坐标，当点O、N、M、H在条直线上时，KM+MN+NK有最小值，最小值=GH；

（3）由平移后的抛物线经过点D，可得到点F的坐标，利用中点坐标公式可求得点G的坐标，然后分为QG=FG、QG=QF，FQ=FQ三种情况求解即可．

试题解析：（1）∵，∴y=（x+1）（x﹣3），∴A（﹣1，0），B（3，0）．

当x=4时，y=，∴E（4，）．

设直线AE的解析式为y=kx+b，将点A和点E的坐标代入得：，解得：k=，b=，∴直线AE的解析式为．

（2）设直线CE的解析式为y=mx﹣，将点E的坐标代入得：4m﹣=，解得：m=，∴直线CE的解析式为．

过点P作PF∥y轴，交CE与点F．

设点P的坐标为（x，），则点F（x，），则FP=（）﹣（）=，∴△EPC的面积=×（）×4=，∴当x=2时，△EPC的面积最大，∴P（2，﹣）．

如图2所示：作点K关于CD和CP的对称点G、H，连接G、H交CD和CP与N、M．

∵K是CB的中点，∴k（，﹣）．

∵点H与点K关于CP对称，∴点H的坐标为（，﹣）．

∵点G与点K关于CD对称，∴点G（0，0），∴KM+MN+NK=MH+MN+GN．

当点O、N、M、H在条直线上时，KM+MN+NK有最小值，最小值=GH，∴GH= =3，∴KM+MN+NK的最小值为3．

（3）如图3所示：

∵y′经过点D，y′的顶点为点F，∴点F（3，﹣）．

∵点G为CE的中点，∴G（2，），∴FG= =，∴当FG=FQ时，点Q（3，），Q′（3，）．

当GF=GQ时，点F与点Q″关于y=对称，∴点Q″（3，）．

当QG=QF时，设点Q1的坐标为（3，a）．

由两点间的距离公式可知：a+=，解得：a=，∴点Q1的坐标为（3，）．

综上所述，点Q的坐标为（3，）或′（3，）或（3，）或（3，）．