题目内容
△ABC中，AB=AC=25cm，高AD=20cm，则BC=分析：△ABC是等腰三角形，AD是底边上的高线，满足三线合一性质，根据勾股定理求出BD的长，再求出BC，代入面积公式即可求解．
解答：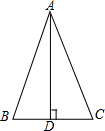
解：∵AD⊥BC
∴在Rt△ABD中，根据勾股定理得到：
BD=
=15cm，
∴BC=2BD=30cm；
S△ABC=
•BC•AD=300cm2．
∴BC=30cm，S△ABC=300cm2．
解：∵AD⊥BC∴在Rt△ABD中，根据勾股定理得到：
BD=
| 252-202 |
∴BC=2BD=30cm；
S△ABC=
| 1 |
| 2 |
∴BC=30cm，S△ABC=300cm2．
点评：本题主要考查了等腰三角形的三线合一的性质，等腰三角形底边上的高线，把等腰三角形分成两个全等的直角三角形．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
如图，在△ABC中，AB=AC，∠A=36°，
15、如图，在△ABC中，AB=AC，点D，E在直线BC上运动．如果∠DAE=l05°，△ABD∽△ECA，则∠BAC=
△ABC中，AB=AC，D、E分别是AB、AC的中点，若AB=4，BC=6，则△ADE的周长是
，连接AO、BE、DC．