题目内容
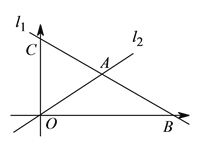
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .
.

(1)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是射线
是射线![]() 上的点,在平面内是否存在点
上的点,在平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)对于直线![]() 解析式,令x=0,求出y的值,确定C的坐标;根据D在直线OA上,设
解析式,令x=0,求出y的值,确定C的坐标;根据D在直线OA上,设![]() ,表示出△COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可;
,表示出△COD面积,把已知面积代入求出x的值,确定出D坐标,利用待定系数法求出CD解析式即可;
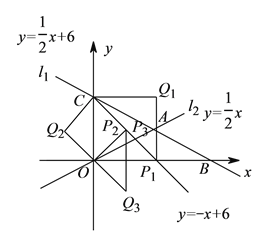
(2)在(1)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:①当四边形![]() 为菱形时,由
为菱形时,由![]() ,得到四边形
,得到四边形![]() 为正方形;②当四边形
为正方形;②当四边形![]() 为菱形时;③当四边形
为菱形时;③当四边形![]() 为菱形时;分别求出Q坐标即可.
为菱形时;分别求出Q坐标即可.
解:(![]() )设
)设![]() .
.
∵![]() 且
且![]() ,
,
∴![]()
∴![]()
∴![]() .
.
令![]() 直线解析式为
直线解析式为![]()
把![]() ,
,![]() 代入得:
代入得:
![]()
∴![]() .
.
∴![]() .
.
(![]() )存在.
)存在.
①当四边形![]() 为菱形时.
为菱形时.
∵![]() 得四边形
得四边形![]() 为正方形
为正方形
∴![]() ,
,
即![]() .
.
②当四边形![]() 为菱形时
为菱形时
∵![]() 得
得![]()
![]() 代入
代入![]() 得
得![]() ,
,
∴![]() .
.
③当四边形![]() 为菱形时
为菱形时
∴![]()
∴![]()
综上得点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目