题目内容
【题目】已知点![]() 是直线
是直线![]() 上的一点,
上的一点,![]() ,射线
,射线![]() 是
是![]() 的一条三等分线,且
的一条三等分线,且![]() .(本题所涉及的角指小于平角的角)
.(本题所涉及的角指小于平角的角)
(1)如图,当射线![]() 、
、![]() 、
、![]() 在直线
在直线![]() 的同侧,
的同侧,![]() ,则
,则![]() 的度数为________;
的度数为________;
(2)如图,当射线![]() 、
、![]() 、
、![]() 在直线
在直线![]() 的同侧,
的同侧,![]() 比
比![]() 的余角大
的余角大![]() ,求
,求![]() 的度数________;
的度数________;
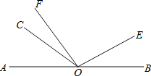
(3)当射线![]() 、
、![]() 在直线
在直线![]() 上方,射线
上方,射线![]() 在直线
在直线![]() 下方,
下方,![]() 小于
小于![]() ,其余条件不变,请同学们自己画出符合题意的图形,探究
,其余条件不变,请同学们自己画出符合题意的图形,探究![]() 与
与![]() 确定的数量关系式,请给出你的结论,并说明理由.
确定的数量关系式,请给出你的结论,并说明理由.
【答案】(1)10°;(2)20°;(3)见解析.
【解析】
(1)由∠BOE=15°,∠COE=120°,求出∠AOE的度数和∠AOC的度数,然后由∠AOF=![]() ∠AOE,求出∠AOF的度数,最后根据角的和差即可求∠COF的度数;
∠AOE,求出∠AOF的度数,最后根据角的和差即可求∠COF的度数;
(2)设∠BOE=x,则∠FOE=130°-x,由∠COE=120°,则∠AOC=60°-x,∠COF=x-10°,进而可求∠AOF=50°,然后由∠AOF=![]() ∠AOE,可求∠AOE的度数,进而可求∠BOE的度数,即x的值,从而可求∠COF的度数;
∠AOE,可求∠AOE的度数,进而可求∠BOE的度数,即x的值,从而可求∠COF的度数;
(3)∠FOC=![]() ∠BOE,画出图形,设∠AOF=x,根据∠AOF=∠AOE,∠COE=120°及角的和差,用含x的式子表示出∠FOC和∠BOE的度数,然后相比即可得到∠FOC=
∠BOE,画出图形,设∠AOF=x,根据∠AOF=∠AOE,∠COE=120°及角的和差,用含x的式子表示出∠FOC和∠BOE的度数,然后相比即可得到∠FOC=![]() ∠BOE.
∠BOE.
(1)![]() ;
;![]() 设
设![]() ,则
,则![]() 的余角为
的余角为![]() ,
,
∵![]() 比
比![]() 的余角大
的余角大![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(3)![]() ,如图所示,
,如图所示,

设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目