题目内容
 如图,在正方形ABCD的外部作等边△DCE,AE交CD于F,则
如图,在正方形ABCD的外部作等边△DCE,AE交CD于F,则| AF |
| FE |
| CF |
| FD |
考点:相似三角形的判定与性质,等边三角形的性质,正方形的性质
专题:
分析:作EH⊥DC于H,设等边△DCE的边长为a,根据等边三角形的性质得CH=DH=
a,DC=DE=a,∠CDE=60°,根据含30度的直角三角形三边的关系得到EH=
DH=
,再根据正方形的性质得AD=DC=a,∠ADC=90°,则AD∥EH,根据相似三角形的判定得到△ADF∽△EHF,根据下似比可解出
=
=
,
则FH=
DF,利用DF+CF=
a,解得DF=(2-
)a,然后计算CF=CD-CF=a-(2-
)a=(
-1)a,再计算
的值.
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| AF |
| EF |
| DF |
| FH |
2
| ||
| 3 |
则FH=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| CF |
| FD |
解答: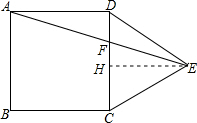 解:作EH⊥DC于H,设等边△DCE的边长为a,如图,
解:作EH⊥DC于H,设等边△DCE的边长为a,如图,
∵△DCE为等边三角形,
∴CH=DH=
a,DC=DE=a,∠CDE=60°,
∴EH=
DH=
,
∵四边形ABCD为正方形,
∴AD=DC=a,∠ADC=90°,
∴AD∥EH,
∴△ADF∽△EHF,
∴
=
,即
=
=
=
,
∴FH=
DF,
∵DF+
DF=
a,解得DF=(2-
)a,
∴CF=CD-CF=a-(2-
)a=(
-1)a,
∴
=
=2
+1.
故答案为
;2
+1.
 解:作EH⊥DC于H,设等边△DCE的边长为a,如图,
解:作EH⊥DC于H,设等边△DCE的边长为a,如图,∵△DCE为等边三角形,
∴CH=DH=
| 1 |
| 2 |
∴EH=
| 3 |
| ||
| 2 |
∵四边形ABCD为正方形,
∴AD=DC=a,∠ADC=90°,
∴AD∥EH,
∴△ADF∽△EHF,
∴
| AF |
| EF |
| DF |
| FH |
| AD |
| EH |
| AF |
| EF |
| DF |
| FH |
| a | ||||
|
2
| ||
| 3 |
∴FH=
| ||
| 2 |
∵DF+
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴CF=CD-CF=a-(2-
| 3 |
| 3 |
∴
| CF |
| FD |
(
| ||
(2-
|
| 3 |
故答案为
2
| ||
| 3 |
| 3 |
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线与其他两边所截的三角形与原三角形相似;相似三角形对应边的比等于相等,都等于相似比.也考查了正方形和等边三角形的性质.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知相交两圆的半径分别为4和7,那么这两圆的圆心距d的取值范围是( )
| A、d>3 |
| B、d<11 |
| C、3<d<11 |
| D、d=3或对11 |
下列各数中,是负分数的是( )
| A、0 | B、-32 |
| C、3.2 | D、-3.2 |
各个数位上数字的立方和等于其本身的三位数叫做“水仙花数”.比如153是“水仙花数”,因为13+53+33=153.以下四个数中是水仙花数的是( )
| A、113 | B、220 |
| C、345 | D、407 |
 在正方形网格中,△ABC的位置如图所示,则sin∠A的值为
在正方形网格中,△ABC的位置如图所示,则sin∠A的值为 如图,为了测量电视塔的高度AB,在D处用高1.2m的测角仪(CD)测得电视塔的顶端A的仰角为36.9°,向电视塔方向前进120m,在F处用测角仪(EF)测得电视塔的顶端A的仰角为67.5°,求这个电视塔的高度AB.(结果精确到1m.参考数据:sin36.9°≈
如图,为了测量电视塔的高度AB,在D处用高1.2m的测角仪(CD)测得电视塔的顶端A的仰角为36.9°,向电视塔方向前进120m,在F处用测角仪(EF)测得电视塔的顶端A的仰角为67.5°,求这个电视塔的高度AB.(结果精确到1m.参考数据:sin36.9°≈