题目内容
已知,点C在以AB为直径的半圆上,∠CAB的平分线AD交BC于点D,⊙O经过A、D两点,且圆心O在AB上.
(1)求证:BD是⊙O的切线.
(2)若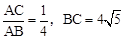 ,求⊙O的面积.
,求⊙O的面积.
【答案】
解:(1)证明:连接OD,

∵AB为直径,∴∠ACB=90°。
∵OA=OD,∴∠ODA=∠OAD。
∵AD平分∠CAB,∴∠OAD=∠CAD。
∴∠ODA=∠CAD。∴OD∥AC。
∴∠ODB=∠ACB=90°。
∴BD是⊙O的切线。
(2)∵ ,∴AB=4AC。
,∴AB=4AC。
∵BC2=AB2﹣AC2, ,∴15AC2=80,解得AC=
,∴15AC2=80,解得AC= 。
。
∴AB=4 。
。
设⊙O的半径为r,
∵OD∥AC,∴△BOD∽△BAC。∴ ,即
,即 。
。
解得:r= 。
。
∴πr2=π•( )2=
)2= 。
。
∴⊙O的面积为 。
。
【解析】
试题分析:(1)连接OD,求出∠CAD=∠OAD=∠ADO,推出OD∥AC,推出OD⊥CB,根据切线判定推出即可。
(2)根据勾股定理求出AC= ,AB=4
,AB=4 .设⊙O的半径为r,证△BOD∽△BAC,得出
.设⊙O的半径为r,证△BOD∽△BAC,得出 ,代入求出r即可。
,代入求出r即可。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
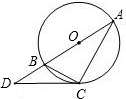 已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.
已知:如图,点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A.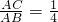 ,
,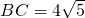 ,求⊙O的面积.
,求⊙O的面积. ,
,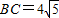 ,求⊙O的面积.
,求⊙O的面积.