题目内容
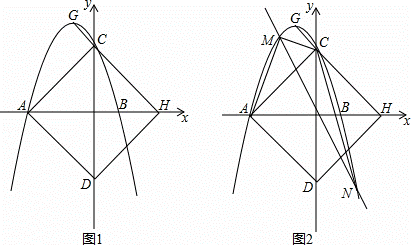
如图,二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),与y轴相交于点C,点G是二次函数图象的顶点,直线GC交x轴于点H(3,0),AD平行GC交y轴于点D.
(1)求该二次函数的表达式;
(2)求证:四边形ACHD是正方形;
(3)如图2,点M(t,p)是该二次函数图象上的动点,并且点M在第二象限内,过点M的直线y=kx交二次函数的图象于另一点N.
①若四边形ADCM的面积为S,请求出S关于t的函数表达式,并写出t的取值范围;
②若△CMN的面积等于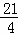 ,请求出此时①中S的值.
,请求出此时①中S的值.
解:(1)∵二次函数y=ax2+bx+3的图象与x轴相交于点A(﹣3,0)、B(1,0),
∴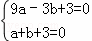
解得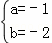
∴二次函数的表达式为y=﹣x2﹣2x+3.
(2)如图1,
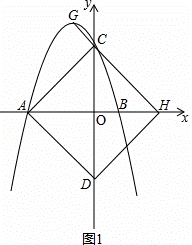 ,
,
∵二次函数的表达式为y=﹣x2﹣2x+3,
∴点C的坐标为(0,3),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴点G的坐标是(﹣1,4),
∵点C的坐标为(0,3),
∴设CG所在的直线的解析式是y=mx+3,
则﹣m+3=4,
∴m=﹣1,
∴CG所在的直线的解析式是y=﹣x+3,
∴点H的坐标是(3,0),
设点D的坐标是(0,p),
则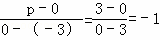 ,
,
∴p=﹣3,
∵AO=CO=DO=HO=3,AH⊥CD,
∴四边形ACHD是正方形.
(3)①如图2,作ME⊥x轴于点E,作MF⊥y轴于点F,
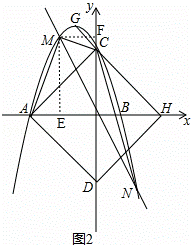 ,
,
∵四边形ADCM的面积为S,
∴S=S四边形AOCM+S△AOD,
∵AO=OD=3,
∴S△AOD=3×3÷2=4.5,
∵点M(t,p)是y=kx与y=﹣x2﹣2x+3在第二象限内的交点,
∴点M的坐标是(t,﹣t2﹣2t+3),
∵ME=﹣t2﹣2t+3,MF=﹣t,
∴S四边形AOCM=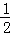 ×3×(﹣t2﹣2t+3)
×3×(﹣t2﹣2t+3)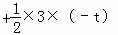 =﹣
=﹣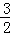 t2﹣
t2﹣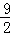 t+
t+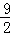 ,
,
∴S=﹣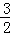 t2﹣
t2﹣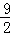 t+
t+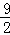 +4.5=﹣
+4.5=﹣ t2﹣
t2﹣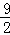 t+9,﹣3<t<0.
t+9,﹣3<t<0.
②如图3,作NI⊥x轴于点I,
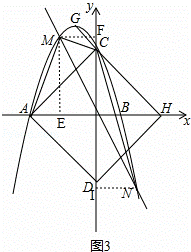 ,
,
设点N的坐标是(t1,p1),
则NI=|t1|,
∴S△CMN=S△COM+S△CON= (|t|+|t1|),
(|t|+|t1|),
∵t<0,t1>0,
∴S△CMN= (|t|+|t1|)=
(|t|+|t1|)=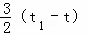 =
=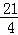 ,
,
 ,
,
联立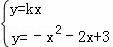
可得x2﹣(k+2)x﹣3=0,
∵t1、t是方程的两个根,
∴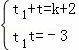
∴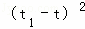 =
=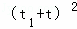 ﹣4t1t=(k+2)2﹣4×(﹣3)=
﹣4t1t=(k+2)2﹣4×(﹣3)=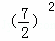 =
=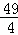 ,
,
解得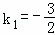 ,
,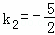 ,
,
a、k=﹣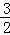 时,
时,
由x2+(2﹣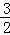 )x﹣3=0,
)x﹣3=0,
解得x1=﹣2,或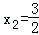 (舍去).
(舍去).
b、k=﹣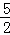 时,
时,
由x2+(2﹣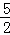 )x﹣3=0,
)x﹣3=0,
解得x3=﹣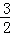 ,或x4=2(舍去),
,或x4=2(舍去),
∴t=﹣2,或t=﹣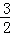 ,
,
t=﹣2时,
S=﹣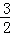 t2﹣
t2﹣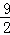 t+9
t+9
=﹣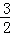 ×4﹣
×4﹣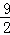 ×(﹣2)+9
×(﹣2)+9
=12
t=﹣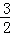 时,
时,
S=﹣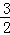 ×
×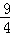 ﹣
﹣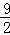 ×
×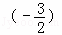 +9
+9
=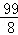 ,
,
∴S的值是12或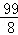 .
.

 步步高达标卷系列答案
步步高达标卷系列答案湘西土家族苗族自治州6月2日至6月8日最高气温(℃)统计如下表:
| 日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 最高气温℃ | 28 | 25 | 25 | 30 | 32 | 28 | 27 |
则这七天最高气温的中位数为( )
A.25℃ B. 27℃ C. 28℃ D. 30℃

 .
.